神经网络初步（Neural Network）——思想 具体实例以及代码实现

　　在前面我们详细的讨论过softmax损失函数以及SVM损失函数，以及应用了支持向量机进行图片分类的任务，不妨先复习一下支持向量机相关的思想内核：支持向量机想要寻求一组映射关系f(x)=wx+b，先将每一个图片的所有像素值都转换成矩阵，然后寻求一个权重矩阵w，使得f(x)=wx+b最后的得分矩阵（或向量）对应了每一个测试数据在每一个类别上的具体分数，最后的决策依据倾向于选择分数最高的类别。我们最后要讨论的便是如何寻找最优的权重矩阵w，我们便引入了一个概念叫做损失函数。

　　首先是svm损失函数，其思想是：对于一个测试数据，我们倾向于正确类别的分数要高于错误类别一定的范围，才不会造成分类有误。换言之，只要我们正确类别的分数高于其他类别一定的安全边界，就可以认为我们没有损失，即图像分类正确；而softmax的思想则是更加类似于将其划归为一个概率事件，将分数取一个指数后归一化，然后根据正确类别的分数判断分类为此类别的概率有多大，将分数取一个负对数后的值作为损失，并以此作为决策依据。可见我们不同的损失函数之间的计算方法虽然不同，但是核心思想都是一样的，即最小化损失函数，那么如何最小化损失函数呢，那便是应用梯度下降去求解，详细请见前文SVM 和 softmax的具体思想。我们支持向量机只要训练出一个较优的权重矩阵即可，我们便可以根据权重矩阵进行矩阵乘法运算，进而进行决策。但是问题也是显而易见的，我们仅仅进行了一次映射，并不能体现更多的细节，所以我们考虑采用多次映射的方法得到最终的分类分数。

　　提到SVM支持向量机，其也可看做是一个最简单的神经网络，他只有一个输入层，然后便是输出信号。我们今天要实现的两层神经网络相较于支持向量机而言多了一个隐藏层，换言之，是经过双层映射得到分数函数，下面先简要介绍一下神经网络的基础知识：

　　首先，人工神经网络是科学家通过研究动物神经元的行为而发明的一种计算模型。动物界的神经元是可以接受并感知外界的刺激，并分泌一种化学物质叫做神经递质，神经递质作用于突触后膜产生电信号，当冲动超过冲动阈值时，便向前面的神经元传递电信号。我们的人工神经网络又分为好多种类，例如前馈神经网络，卷积神经网络等，详细的分类见下图

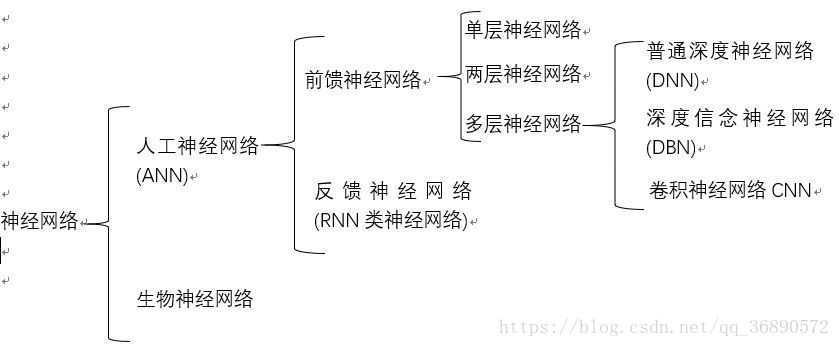
（图片源自水印）

　　那么每个神经元之间是如何建立联系的呢？我们看下图，首先中间的圆圈是神经元，也是神经网络最小的组成单元（unit），以下图片深度模拟了生物体内神经元接受刺激传递兴奋的过程：首先是神经元接受不同的信号刺激，每一种信号对神经元刺激的程度不同，即对于不同的输入数据对有不同贡献即权重不同；在拟合完权重后加上偏差项（bias），将此值与阈值比较，如果超过阈值那么就会向前传播产生信号，那么传播的信号便是通过激活函数映射产生的值，即f(sigma(wixi)+b)。不同层之间的神经元便靠着这种激活函数进行分数或者函数值的传递。通常情况下激活函数都是非线性函数，那么为什么我们需要用非线性函数作为激活函数呢？如果我们不用非线性函数，而采用线性函数，那么最后我们的输出层输出的结果仍然是输入的线性组合，那么也就失去了我们引入隐藏层的意义：我们引入隐藏层是为了使模型能够逼近任意真实函数，这样使得我们的分类亦或是其他任务的泛化能力尽可能的强，能够解决更多情境下的非线性问题，所以我们所有的激活函数都是非线性的。

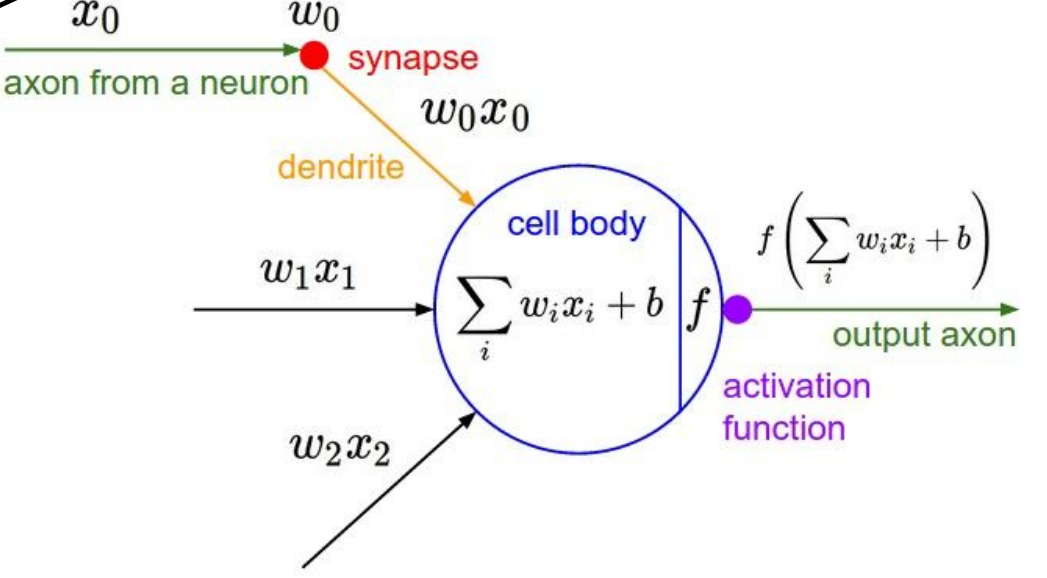
　　显然，决定我们神经网络性能的因素除去前面SVM中的不同超参数，还多了一种，便是激活函数的选取，目前有Sigmoid，Leaky ReLU，ReLU，Maxout，TanH等等，不同的激活函数具有不同的适用场景，下面将说明这一点：

　　1.sigmoid函数

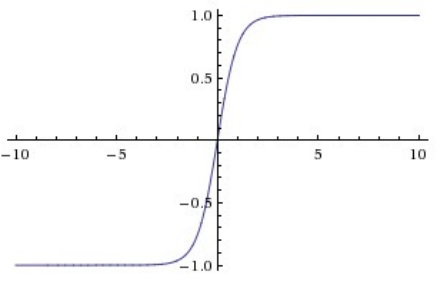
　　我们知道sigmoid函数的解析式为σ(x) = 1/(1 + e −x )，其图像如图所示：显然，我们从图像中可以看出一个问题：那便是在我们的x充分大或者充分小时，函数的导数过于小，即梯度很小，这便导致我们在日后进行随机梯度下降寻求最好的超参数时很容易陷入无解的状态，即梯度下降过于小导致学习速率降低甚至无法找到最优的超参数或权重矩阵。但是sigmoid函数在历史上属于非常优越的地位，因为它将任意一个数x都可以压缩到[0,1]这个区间范围内，并且它的工作模式更加贴近于真实神经元的工作情况，能够很好的模拟神经元的放电率；此外，由于它将任意一个数x都能压缩到[0,1]的区间内，可以有效避免在多层计算中导致数值过度膨胀等问题。但是其劣势也是显而易见的，刚刚我们讨论了其中一点：梯度的值在|x|很大的情况下很小，这就导致了我们在随机梯度下降的过程中收敛速度过慢，训练时间可能非常长。sigmoid模型由于可以将任意输入压缩为[0,1]之间的数故更加适用于以概率作为输出的情景。

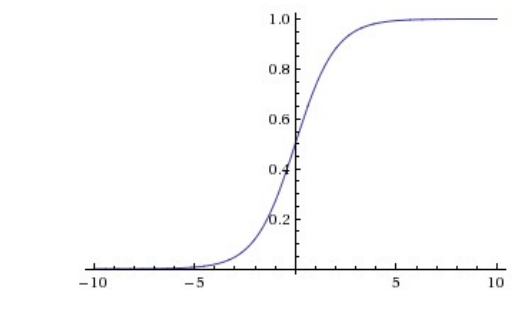
　　2.ReLU函数

　　ReLU函数的解析式为：f(x) = max(0, x)，其图像如下图所示。目前而言，ReLU函数变得及其的流行，其特点为：对于任意的x>0，其梯度均为1.梯度无论x有多大，都是一个常数，换言之，在SGD随机梯度下降中，其收敛速率要显著的快于Sigmoid函数以及下文将要提到的Tanh；此外，ReLU的计算速率奇快无比，只需要计算max函数就行，相较于计算机计算Tanh或者Sigmoid的指数形式，都要快上不少，我们的时间代价小很多。同样的，ReLU函数也具有一定的缺陷——神经元死亡：我们考虑SGD随机梯度下降更新我们权重矩阵w的算法：w=w-learning_rate*dw，我们的dw便是当前损失函数的梯度，我们ReLU函数的梯度恒为1，那么当learning_rate比较大且当前的w比较小时便会出现w被更新为负数的情况，而w更新为负数，那么我们wx相乘也为负数，根据ReLU激活函数，其梯度一直为0，这就会导致w一直不会被更新，此便称之为神经元的死亡。但是很显然，我们采用ReLU时完全可以采用减小学习率（步长）去缓解神经元死亡的现象。

　　3.Leaky ReLU

　　Leaky ReLU和ReLU相比较，其x>0时输出x不变，当x小于0时，输出kx，其中k的选取是任意的，通常我们选取0.01/0.1，其图像如下图所示。相比于ReLU，我们的leaky ReLU解决了神经元死亡这一问题。我们神经元死亡的问题是由于当w<0过后，ReLU函数的导数始终为0，那么在之后的链式法则传递过程中gradient恒为0导致w始终无法被更新，而我们的Leaky ReLU在x<0时的梯度为k，所以就算有一步w<0了，在过后的更新中也能挽救回来，不至于整个神经元直接无法传递信息更新梯度。这个函数理论上具有ReLU的全部优点并且弥补了ReLU的缺点，应该泛用性很广，但是在实践中我们发现他的性能并不稳定，所以很难得到广泛的应用。

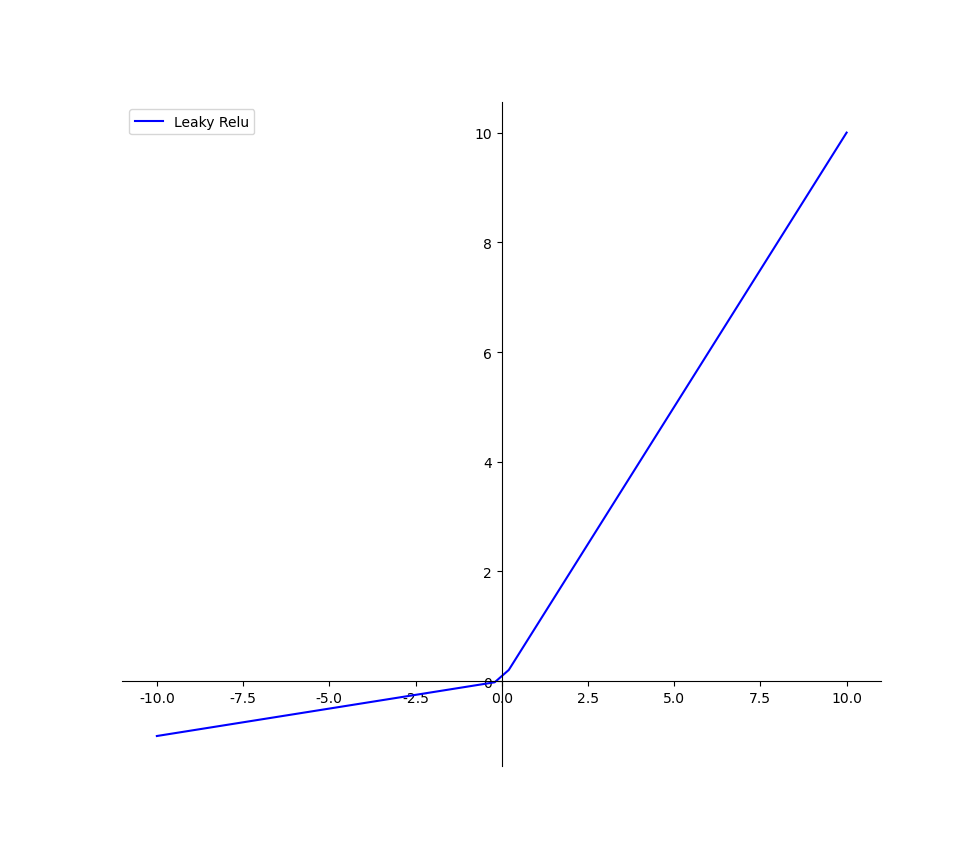
　　4. Tanh函数

　　

　　

　　Tanh的解析式为：tanh(x) = 2σ(2x) − 1.上图为Tanh的图像，显然，它和sigmoid函数具有很多的相似之处，都可以把输入数据压缩，不过不同的是，Tanh将任意输入压缩为[-1,1]上的数，而sigmoid压缩为[0,1]上的数，他们的缺点都是共同的，就是随机梯度下降的过程中收敛速度过慢，训练时间可能非常长。但是Tanh函数相比较与sigmoid函数有相应的优点：它输出的均值是0，可以不改变输入数据原本的分布情况，此外，Tanh的梯度取值在[0,1]之间，可以缓解梯度消失问题（但是这个问题在|x|充分大时仍然存在）。此外，由于Tanh是有sigmoid函数计算得到的，所以仍然存在幂运算速率较慢等因素。

 

 

　　5. Maxout函数

　　

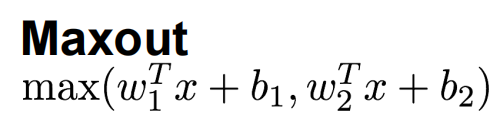
　　上图展示了Maxout函数的解析式，显然，我们ReLU解析式是Maxout的特殊形式，即w1=b1=0的特例。Leaky ReLU同样也是Maxout的一个特例。相较于我们上文提到的激活函数，他们都没有非线性应用权重矩阵和输入数据矩阵点积的形式。Maxout计算的便是不同的权重矩阵计算出分数的较大值。由于Maxout函数包涵了ReLU以及Leaky ReLU，所以他享受有所有ReLU以及Leaky ReLU的优点，并且解决了神经元死亡的问题，不过相应的，也有问题存在，那便是增加了运算以及超参数的复杂度，每个节点的参数都翻倍了，这就导致了总体参数数量非常多，增加了运算的复杂度。

　　All in All，不同的激活函数具有不同的适用范围，使用ReLU激活函数时，要注意学习率，并监控网络中神经元死亡的比例。如果你担心，试一下Leaky ReLU或Maxout。切勿使用sigmoid。试试tanh，但期望上，它比ReLU/Maxout效果要糟糕一些。

　　在介绍完神经网络的具体思想后，我们开始重头戏，搭建一个Two_Layer-Net，并且是一个Fully-Conncted_Neural Network，在这之前，我们先来了解一下什么是全连接神经网络：相邻两层之间任意两个节点之间都有连接。全连接神经网络是最为普通的一种模型（比如和CNN相比），由于是全连接，所以会有更多的权重值和连接，因此也意味着占用更多的内存和计算。本次的搭建双层全连接神经网络为CS231N课程作业Assignment1中的Two_Layer-Net的实战测试，相应的，会附加上代码和思路解析。

　　在作业中，要求我们应用模块化的方法实现全连接网络，对于神经网络的任意一层，我们都需要完成前向传播和反向传播两个模块，前向传播需要我们输入数据，权重矩阵和一些超参数，并计算出映射函数的具体函数值，然后返回输出值和必要的中间变量，这个中间变量便是我们需要在BP传播中用到的（BP原理详见上条博客），那么前向传播的代码就如下所示（示例）

 1 def layer_forward(x, w):
 2   """ Receive inputs x and weights w """
 3   # Do some computations ...
 4   z = # ... some intermediate value
 5   # Do some more computations ...
 6   out = # the output
 7
 8   cache = (x, w, z, out) # Values we need to compute gradients
 9
10   return out, cache
11
12
13   

Layer_forward

　　反向传播的思路详见https://www.cnblogs.com/Lbmttw/p/16844897.html，其代码示例如下：

 1 def layer_backward(dout, cache):
 2   """
 3   Receive dout (derivative of loss with respect to outputs) and cache,
 4   and compute derivative with respect to inputs.
 5   """
 6   # Unpack cache values
 7   x, w, z, out = cache
 8
 9   # Use values in cache to compute derivatives
10   dx = # Derivative of loss with respect to x
11   dw = # Derivative of loss with respect to w
12
13   return dx, dw

layer_backward

　　在我们实现不同层过后，我们就可以很轻松的将他们组合起来，形成全连接双层神经网络：

　　考虑我们向前传播的全连接映射层映射函数的写法：在这个函数中，我们需要计算前向传播的函数值，在这里我们需要输入三组数据，第一组为x，即我们的训练数据，其形状为N*d1*d2*...*dk，d1-dk为x[i]每一个维度的属性值，我们需要将其转化为一个维度为D的向量，即将其变为N*D的一个矩阵。在前向传播中，我们需要计算wx+b的函数值，并且将其向前传播，同时在cache中缓存当前节点输入的数据，当前节点的权重矩阵以及偏差项，所以很轻松能够写出一下的代码：

1 def affine_forward(x, w, b):
2     out = None
3     num_train=x.shape[0]
4     num_class=w.shape[1]
5     x_new=np.reshape(x,(num_train,-1))
6     out=x_new.dot(w)+b
7     cache = (x, w, b)
8     return out, cache

affine_forward(x, w, b):

　　写完前向传播过后，我们考虑反向传播：BP的过程便是计算出当前节点的梯度值并将其传输给前一个节点，所以，我们的输入应当有上一个节点的导数值dout，以及当前节点的缓存cache，返回的值则是当前节点的梯度值：即当前的dx,dw以及db（因为这里的分数函数是关于w，x，b的一个函数，我们要分别求出df/dw,df/dx,df/db）。由于我们的f=wx+b，则我们当前节点对于b求偏导的结果就是1，则输出的db应当与前一个节点的dout有关。而对于向量乘法的f=wx，我们对于x求偏导的结果就是w，所以dx的结果是dout*w，由于我们矩阵相乘的结果是N*D，我们需要返回数组的形状为N*d1*d2*...*dk，即与输入数据的形状相同，于是我们便需要对原本的数组进行reshape操作；而考虑对w求偏导：其结果是x的转置，由于b是偏差项，我们可以暂时不考虑，我们考虑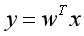，其梯度结果具体证明过程如下：

　　我们由上文的证明过程，可以知道我们当前的映射函数对于x求偏导的结果是权重矩阵的转置，同理，对权重矩阵求偏导的结果是输入的转置。于是我们可以很容易写出下面的代码：

1 def affine_backward(dout, cache):
2     x, w, b = cache
3     dx=dout.dot(w.T)
4     dx=np.reshape(dx,(dx.shape[0],*x.shape[1:]))
5     #在这里reshape的用途是将N*D的矩阵reshape为（N，d1，…，d_k），*x.shape[1:]中*是取d1-dk中所有值，以无括号的形式输出
6     temp=np.reshape(x,(x.shape[0],-1))
7     dw=temp.T.dot(dout)
8     db=np.sum(dout,axis=0)
9     return dx, dw, db

def affine_backward(dout, cache)

　　

　　我们至此，已经完成了神经元的前向传播和BP过程，我们接下来考虑神经网络不同层之间的链接：即激活函数的写法，我们在这类采用ReLU：显然，在这里我们需要经过当前神经元的分数函数，然后输出一个经过ReLU函数映射后的函数，同时，我们还应该在这里暂时性的储存中间值，那么ReLU的写法如下：

1 def relu_forward(x):
2     out=np.where(x>0,x,0)
3     #where（x,y,z） 其中x是条件，如果x为真，则为y，否则为z
4     cache = x
5     return out, cache

　　同样的，我们也需要在ReLU函数中计算反向传播后的梯度值，只要我们前向映射过，那么反向传播中计算的梯度就应当考虑到映射节点：显然，此处的映射函数是ReLU型。如果此时的输入大于0，梯度是1，传递给下一个节点的梯度值就是上一个节点流向此节点的值，即dout，如果此时输入的值小于等于0，那么此时的梯度值就是0。那么我们的算法如下：

1 def relu_backward(dout, cache):
2     dx, x = None, cache
3     dx=np.where(x>0,dout,0)
4     pass
5     return dx

def relu_backward(dout, cache):

　　之后，完成了基本的模块化的初始化过程，我们就可以开始计算损失函数了，同样的，在这里我们提供SVM以及softmax两种损失函数的写法。

　　具体SVM，softmax的思路详见https://www.cnblogs.com/Lbmttw/p/16844897.html以及https://www.cnblogs.com/Lbmttw/p/16830180.html

 1 def svm_loss(x, y):
 2     num_train=x.shape[0]
 3     num_class=x.shape[1]
 4        correct_score=x[np.arange(num_train),y].reshape(num_train,1)
 5     Li=np.maximum(0,x-correct_score+1)
 6     Li[np.arange(num_train),y]=0
 7     loss=np.sum(Li)/num_train
 8     Li[Li>0]=1
 9     sigma=np.sum(Li,axis=1)
10     Li[np.arange(num_train),y]-=sigma
11     dx=Li/num_train
12     return loss, dx

def svm_loss(x, y):

 1 def softmax_loss(x, y):
 2     loss, dx = 0.0, None
 3     num_train=x.shape[0]
 4     x=np.exp(x)
 5     temp=np.sum(x,axis=1)
 6     soft_max=x/temp.reshape(num_train,1)
 7     loss_i=-np.sum(np.log(soft_max[np.arange(num_train),y]))
 8     loss+=loss_i
 9     loss/=num_train
10     soft_max[np.arange(num_train),y]-=1
11     dx=soft_max/num_train
12     return loss, dx

　　之后我们考虑应用先前写过的代码去搭建一个两层的全连接神经网络：此神经网络的架构是经过affine_ReLU------affine_softmax。我们在下面的类中实现数据的存储，初始化的步骤：在这里面我们输入若干个数据分别为：

　　input_dim: An integer giving the size of the input 给出输入数据的规模

       hidden_dim: An integer giving the size of the hidden layer 隐藏网络的规模（可以认为是有多少个神经节点）

       num_classes: An integer giving the number of classes to classify 共有多少个类

       weight_scale: Scalar giving the standard deviation for random initialization of the weights. 给出权重初始化的标准偏差。

       reg: Scalar giving L2 regularization strength.L2正则项

　　同时，在这里我们将初始化双层神经网络的权重和偏差项，同时初始化权重矩阵：服从N(0,weight_scale)，偏差初始化为零。所有权重和偏差都应存储在self.params中。第一层权重矩阵和偏差使用关键字“W1”和“b1”，第二层神经网络的权重矩阵和偏差使用关键字“W2”和“b2”。（类似于Hash）那么我们就很简单能写出以下的代码：

 1 def __init__(
 2         self,
 3         input_dim=3 * 32 * 32,
 4         hidden_dim=100,
 5         num_classes=10,
 6         weight_scale=1e-3,
 7         reg=0.0,
 8     ):
 9      self.params['W1']=np.random.normal(loc=0,scale=weight_scale,size=(input_dim,hidden_dim))
10         self.params['b1']=np.zeros(hidden_dim)
11         self.params['W2']=np.random.normal(loc=0,scale=weight_scale,size=(hidden_dim,num_classes))
12         self.params['b2']=np.zeros(num_classes)

def __init__

　　然后我们完成类中的两层神经网络的前向传播损失函数的计算（在这里我们只需要调用之前所写过的函数即可）：在这里，我们需要输入训练数据X，以及训练数据X所对应的标签y，我们需要计算出每一个X的分数y，并且将其存储到score中，我们在这个函数中，需要返回损失函数的值，以及不同参数的梯度，值得注意的是，不同参数的梯度我们都存储在同一个数组中，同样的，我们第一层权重矩阵和偏差使用关键字“W1”和“b1”，第二层神经网络的权重矩阵和偏差使用关键字“W2”和“b2”。所以我们可以写出一下代码：

　　值得注意的是我们的传播过程是输入层------第一层神经网络映射（输出out1）-------ReLU映射到第二层（输出out2）------第二层（hidden layer）映射到输出层（输出out3），所以我们最后的分数函数是out3，我们计算损失则需要对out3计算（因为计算损失必须得在分数函数出炉后才能计算，在这里out3就是我们的分数函数）。在out3过后，处理办法就和我们SVM线性分类器完全一致了。别忘了，我们还有L2正则项需要处理在损失函数中。

　　在处理完这些过后，我们就可以使用BP算法计算梯度：我们从输出层-------第二层-------ReLU--------第一层--------开头这个顺序来进行反向求梯度，首先我们在上面前向传播的时候，已经存储好若干的中间值，我们在反向传播的时候可以直接将这些中间值全部传到函数中即可。我们在计算损失函数时，已经将x的梯度dx计算出来，所以我们可以直接将dx作为dout传输到第二层的affine_backward中，同时更新dx，然后将其传输到ReLU_backward中，继续更新dx，最后我们将dx和最开始的缓存cache1继续进行affine_backward。就这样，我们计算出来了w2,b2,w1,b1所有的梯度值，别忘记加入正则项即可，attention！由于我们b的梯度只与之前的输入有关，至多不大于之前的输入，所以不用加正则项防止梯度爆炸和过拟合的现象。

 1 def loss(self, X, y=None):
 2  out1,cache1=affine_forward(X,self.params['W1'],self.params['b1'])
 3         out2,cache2=relu_forward(out1)
 4         out3,cache3=affine_forward(out2,self.params['W2'],self.params['b2'])
 5         loss,dx=softmax_loss(out3,y)
 6         loss+=0.5*self.reg*(np.sum(self.params['W1']*(self.params['W1']))+np.sum(self.params['W2']*self.params['W2']))
 7         scores=out3
 8         dx,grads['W2'],grads['b2']=affine_backward(dx,cache3)
 9         dx=relu_backward(dx,cache2)
10         m,grads['W1'],grads['b1']=affine_backward(dx,cache1)
11         grads['W2']+=grads['W2']*self.reg
12         grads['W1']+=grads['W1']*self.reg
13         return loss, grads

def loss(self, X, y=None):

　　我们考虑开始训练一个模型，我们需要编写一个大的solver类用于训练模型，其中solver类中包括了不同的成员函数：Init（初始化函数），reset函数（用于记录一些用于优化的变量，注意，这个reset函数不要手动调用），step函数（用于进行单一的梯度更新，同样，这个step函数也不要手动调用，这个函数会在train函数中进行调用），check_accuracy函数（用于检查模型预测的准确性），最后就是我们的train函数，train函数的作用就是优化模型，训练模型。值得注意的是，我们编写的Solver类中是不包括优化模型相应的更新方法的，我们需要需要手动编写一些更新方法函数以便于在solver类中调用，在本文中，我们不妨先考虑几个可能会用到的优化规则以及其写法：

　　第一个就是随机梯度下降，随机梯度下降的原理在前文说的很清楚了，我们在此处不赘述了，直接说代码的参数，sgd（随机梯度下降函数）中需要包涵当前的待优化变量也即权重矩阵，然后还有当前的梯度值，那么很容易给出代码（由于随机梯度下降的公式为w'=w-dw*learning_rate，所以代码编写异常简单）：需要注意的是，此处的config中的learning_rate需要我们提前赋予初值，config里面存储好多变量，每一个变量都具有相应的值，类似于哈希表的存储读取方式。

1 def sgd(w, dw, config=None):
2     if config is None:
3         config = {}
4     config.setdefault("learning_rate", 1e-2)
5     w -= config["learning_rate"] * dw
6     return w, config

sgd

　　之后就是sgd_momentum，容易理解的方法说，就是优化版的随机梯度下降；那么相较于sgd，其到底优化了什么地方呢？sgd_momentum优化了sgd的收敛过程，换言之，使其迭代次数减少。解决了部分情况下随机梯度下降无法得到最优解的问题（此时为震荡状态）。sgd_momentum仅仅多了一个超参数，该参数控制梯度下降公式中的动量。

　　更具体的代码实现过程和定理的说明部分将新开一个博客单独说明，不占用神经网络的篇幅。在这里我们应用sgd更新。

　　实现好梯度的更新法则后，我们分别来考虑solver类中的几个成员函数（下面为Init函数），在说明此函数之前，我们先对solver类进行说明：这个类封装了可能用到的所有函数，在这里我们仅用sgd随机梯度下降来更新我们的权重矩阵；solver类中接收训练数据和验证数据，可以定期的根据训练数据和验证数据的准确性来判断是否产生过拟合现象。同时，如果我们想要训练一个模型，我们就需要先构造一个solver的实例，给出相应的参数（如数据集，学习率等），然后我们就可以调用train函数来训练优化一个模型了。在train函数返回后，np数组model.params中包涵了在整个训练过程中表现最好的一组超参数，此外，loss_history将包涵训练过程中所有的损失函数的具体值以及相应的变量值。solver.train_acc和solver_train_val_acc是在每一轮测试集和训练集上表现最好的那组超参数所对应的准确率。我们在调用的时候类似于：

 1     data = {
 2       'X_train': # training data
 3       'y_train': # training labels
 4       'X_val': # validation data
 5       'y_val': # validation labels
 6     }
 7     model = MyAwesomeModel(hidden_size=100, reg=10)
 8     solver = Solver(model, data,
 9                     update_rule='sgd',
10                     optim_config={
11                       'learning_rate': 1e-4,
12                     },
13                     lr_decay=0.95,
14                     num_epochs=5, batch_size=200,
15                     print_every=100)
16     solver.train()

example

　　此外，我们的solver实例必须符合相应的规则，如model.params是一个np数组，将字符串参数作为关键字存储相应超参数；model.loss(x,y)中的x，y分别是小批量的测试数据以及测试数据所对应的标签，我们在调用loss时，返回值是对应的损失函数值以及相应的梯度（同样应将字符串参数作为关键字存储梯度）。知晓约定俗成的规则后，我们先来考虑初始化的代码：

 1 def __init__(self, model, data, **kwargs):
 2         self.model = model
 3         self.X_train = data["X_train"]
 4         self.y_train = data["y_train"]
 5         self.X_val = data["X_val"]
 6         self.y_val = data["y_val"]
 7         self.update_rule = kwargs.pop("update_rule", "sgd")
 8         self.optim_config = kwargs.pop("optim_config", {})
 9         self.lr_decay = kwargs.pop("lr_decay", 1.0)
10         self.batch_size = kwargs.pop("batch_size", 100)
11         self.num_epochs = kwargs.pop("num_epochs", 10)
12         self.num_train_samples = kwargs.pop("num_train_samples", 1000)
13         self.num_val_samples = kwargs.pop("num_val_samples", None)
14
15         self.checkpoint_name = kwargs.pop("checkpoint_name", None)
16         self.print_every = kwargs.pop("print_every", 10)
17         self.verbose = kwargs.pop("verbose", True)
18         if len(kwargs) > 0:
19             extra = ", ".join('"%s"' % k for k in list(kwargs.keys()))
20             raise ValueError("Unrecognized arguments %s" % extra)
21         if not hasattr(optim, self.update_rule):
22             raise ValueError('Invalid update_rule "%s"' % self.update_rule)
23         self.update_rule = getattr(optim, self.update_rule)
24         self._reset()

init

　　在初始化中，我们需要初始的元素有

　　   update_rule: A string giving the name of an update rule in optim.py. 在这里，我们的参数可以是在其余函数中写过的优化规则的函数名称，默认是sgd

          optim_config: A dictionary containing hyperparameters that will be passed to the chosen update rule.

          Each update rule requires different hyperparameters (see optim.py) but all update rules require a 'learning_rate' parameter so that should always be present.

　　   这里面的索引是超参数的名称，其值是超参数的值

 

          lr_decay: A scalar for learning rate decay; after each epoch the learning rate is multiplied by this value.学习率衰减量，每次迭代后学习率都减少lr_decay

          batch_size: Size of minibatches used to compute loss and gradient during training. 小批量测试集样本的数量

          num_epochs: The number of epochs to run for during training.进行训练的轮数

          print_every: Integer; training losses will be printed every print_every iterations.训练的损失将会被在每次print_every次迭代中输出出来（每训练多少个训练数据输出一次损失值）

          verbose: Boolean; if set to false then no output will be printed during training.是一个布尔类型的变量，用于判断在训练中是否输出

          num_train_samples: Number of training samples used to check training accuracy; default is 1000; set to None to use entire training set. 训练集的数目

          num_val_samples: Number of validation samples to use to check val accuracy; default is None, which uses the entire validation set.验证集的数目

          checkpoint_name: If not None, then save model checkpoints here every epoch.将checkpoint的名称存储在这里

　　

　　初始化过后我们来看reset，重置函数：

 1 def _reset(self):
 2         self.epoch = 0
 3         self.best_val_acc = 0
 4         self.best_params = {}
 5         self.loss_history = []
 6         self.train_acc_history = []
 7         self.val_acc_history = []
 8         self.optim_configs = {}
 9         for p in self.model.params:
10             d = {k: v for k, v in self.optim_config.items()}
11             self.optim_configs[p] = d

reset

　　需要注意的只要两个地方：

　　1.reset函数不能手动调用，是重置数据和模型的

　　2.我们要对每一个超参数在optim_config中进行深拷贝

　　最重要的是下面接下来要说的几个函数，首先是step函数，在step中我们要进行一次梯度的更新，只要实现一次梯度更新，那么我们就能实现n次更新，所以在重复的迭代更新中最重要的就是找到如何更新单次梯度：

 1     def _step(self):
 2         num_train = self.X_train.shape[0]
 3         batch_mask = np.random.choice(num_train, self.batch_size)
 4         X_batch = self.X_train[batch_mask]
 5         y_batch = self.y_train[batch_mask]
 6         loss, grads = self.model.loss(X_batch, y_batch)
 7         self.loss_history.append(loss)
 8         for p, w in self.model.params.items():
 9             dw = grads[p]
10             config = self.optim_configs[p]
11             next_w, next_config = self.update_rule(w, dw, config)
12             self.model.params[p] = next_w
13             self.optim_configs[p] = next_config

def _step(self):

　　首先，在这个函数中，我们要先新建一个小批量的训练集用于测试他的损失函数以及相应的梯度值，与上文一样的，我们需要将损失值以及梯度值存储到model所对应的np数组中便于后续输出查看（就算不存储也对找到最优解无关，只不过存储是为了让每一轮次的训练结果可视化而已）。对于最下面的循环，他的参数表（params）是在最上面的初始化中（神经网络搭建那部分的初始化中）得到的，其中，p为对应的索引即他的名称（如上文提到的w1,b1这些），那么这个循环的功能就很显而易见了，用于更新我们的权重矩阵的值，更新方法是：首先获取我们权重矩阵目前的梯度，然后利用update_rule中定义的规则来进行更新（在这里定义的规则只定义了sgd随机梯度下降，所以我们调用的就是随机梯度下降的代码）得到更新后的权重矩阵值，我们将更新后的值存到params的数组中，其索引是p。如此就实现了单次更新目前所有层所对应的超参数的值。

　　在更新完我们需要做的就是保存操作，利用的是如下的代码：

 1 def _save_checkpoint(self):
 2         if self.checkpoint_name is None:
 3             return
 4         checkpoint = {
 5             "model": self.model,
 6             "update_rule": self.update_rule,
 7             "lr_decay": self.lr_decay,
 8             "optim_config": self.optim_config,
 9             "batch_size": self.batch_size,
10             "num_train_samples": self.num_train_samples,
11             "num_val_samples": self.num_val_samples,
12             "epoch": self.epoch,
13             "loss_history": self.loss_history,
14             "train_acc_history": self.train_acc_history,
15             "val_acc_history": self.val_acc_history,
16         }
17         filename = "%s_epoch_%d.pkl" % (self.checkpoint_name, self.epoch)
18         if self.verbose:
19             print('Saving checkpoint to "%s"' % filename)
20         with open(filename, "wb") as f:
21             pickle.dump(checkpoint, f)

_save_checkpoint

　　在这里，没什么注意事项，在save函数中仅仅是判断verbose来判定是否输出并且存储相应参数到一个文件中而已，与算法本身无关，我们不关注，直接来看check函数：

 1 def check_accuracy(self, X, y, num_samples=None, batch_size=100):
 2         N = X.shape[0]
 3         if num_samples is not None and N > num_samples:
 4             mask = np.random.choice(N, num_samples)
 5             N = num_samples
 6             X = X[mask]
 7             y = y[mask]
 8         num_batches = N // batch_size
 9         if N % batch_size != 0:
10             num_batches += 1
11         y_pred = []
12         for i in range(num_batches):
13             start = i * batch_size
14             end = (i + 1) * batch_size
15             scores = self.model.loss(X[start:end])
16             y_pred.append(np.argmax(scores, axis=1))
17         y_pred = np.hstack(y_pred)
18         acc = np.mean(y_pred == y)
19
20         return acc

check_accuracy

　　在这个函数中，我们根据输入数据判定模型的准确率，输入测试的图片，以及相应的标签。num_sample的用处是判断是否需要在样本中进行子采样，如果其不为0，并且我们当前输入的样本的数量要多于我们进行测试的数量（num_sample），那么我们就需要在输入样本中进行二次采样。之后的代码就是判断模型的准确率了，返回值是在当前的测试集上的准确率（代码中//的意义是向下取整（类似于C++中的整数除法））

　　最后一个函数式是整个类中最重要的函数：train函数，训练出一个神经网络模型，也就是说我们在这里需要调用优化程序来训练出一个分类器，我们先来看代码：

 1 def train(self):
 2         num_train = self.X_train.shape[0]
 3         iterations_per_epoch = max(num_train // self.batch_size, 1)
 4         num_iterations = self.num_epochs * iterations_per_epoch
 5         for t in range(num_iterations):
 6             self._step()
 7             if self.verbose and t % self.print_every == 0:
 8                 print(
 9                     "(Iteration %d / %d) loss: %f"
10                     % (t + 1, num_iterations, self.loss_history[-1])
11                 )
12
13             epoch_end = (t + 1) % iterations_per_epoch == 0
14             if epoch_end:
15                 self.epoch += 1
16                 for k in self.optim_configs:
17                     self.optim_configs[k]["learning_rate"] *= self.lr_decay
18
19             # Check train and val accuracy on the first iteration, the last
20             first_it = t == 0
21             last_it = t == num_iterations - 1
22             if first_it or last_it or epoch_end:
23                 train_acc = self.check_accuracy(
24                     self.X_train, self.y_train, num_samples=self.num_train_samples
25                 )
26                 val_acc = self.check_accuracy(
27                     self.X_val, self.y_val, num_samples=self.num_val_samples
28                 )
29                 self.train_acc_history.append(train_acc)
30                 self.val_acc_history.append(val_acc)
31                 self._save_checkpoint()
32                 if self.verbose:
33                     print(
34                         "(Epoch %d / %d) train acc: %f; val_acc: %f"
35                         % (self.epoch, self.num_epochs, train_acc, val_acc)
36                     )
37                 if val_acc > self.best_val_acc:
38                     self.best_val_acc = val_acc
39                     self.best_params = {}
40                     for k, v in self.model.params.items():
41                         self.best_params[k] = v.copy()
42         self.model.params = self.best_params

train

　　函数部分特别长，iterations_per_epoch的意义是一共需要迭代多少次，那么迭代次数要么是1，要么是总数/每次轮换的个数，所以我们进行一个取最大值的运算就能得到；那么总迭代次数就是训练的轮数*每一次的迭代次数；我们在每次的迭代过程中，都需要更新我们的超参数，所以就需要调用step函数；同时，在训练完100个样本后，输出一次损失函数，在每次训练完500个样本后（即训练完一轮），输出一次当前的在训练集上的准确率和在测试集（验证集）上的准确率。别忘了在训练过程中，每次的学习率都要衰减。每完成一次训练，我们都需要去更新一次当前最优的参数是什么以及相应的准确率，所对应的就是代码中最后的部分。同时，我们将model中存储的参数更新为当前最优的参数，用于后续测试集的测试。

　　至此，我们所有模块化的神经网络组件就已经全部完成，我们可以组装起来：

 1 input_size = 32 * 32 * 3
 2 hidden_size = 50
 3 num_classes = 10
 4 model = TwoLayerNet(input_size, hidden_size, num_classes)
 5 solver = None
 6 solver=Solver(model, data,
 7        update_rule='sgd',
 8        optim_config={
 9         'learning_rate': 1e-3,
10        },
11        lr_decay=0.95,
12        num_epochs=10, batch_size=100,
13        print_every=100)
14 solver.train()
15 print(solver.check_accuracy(data['X_test'], data['y_test']))

Part1

　　在训练完后，我们可以将训练结果可视化出来，得到以下的图表：

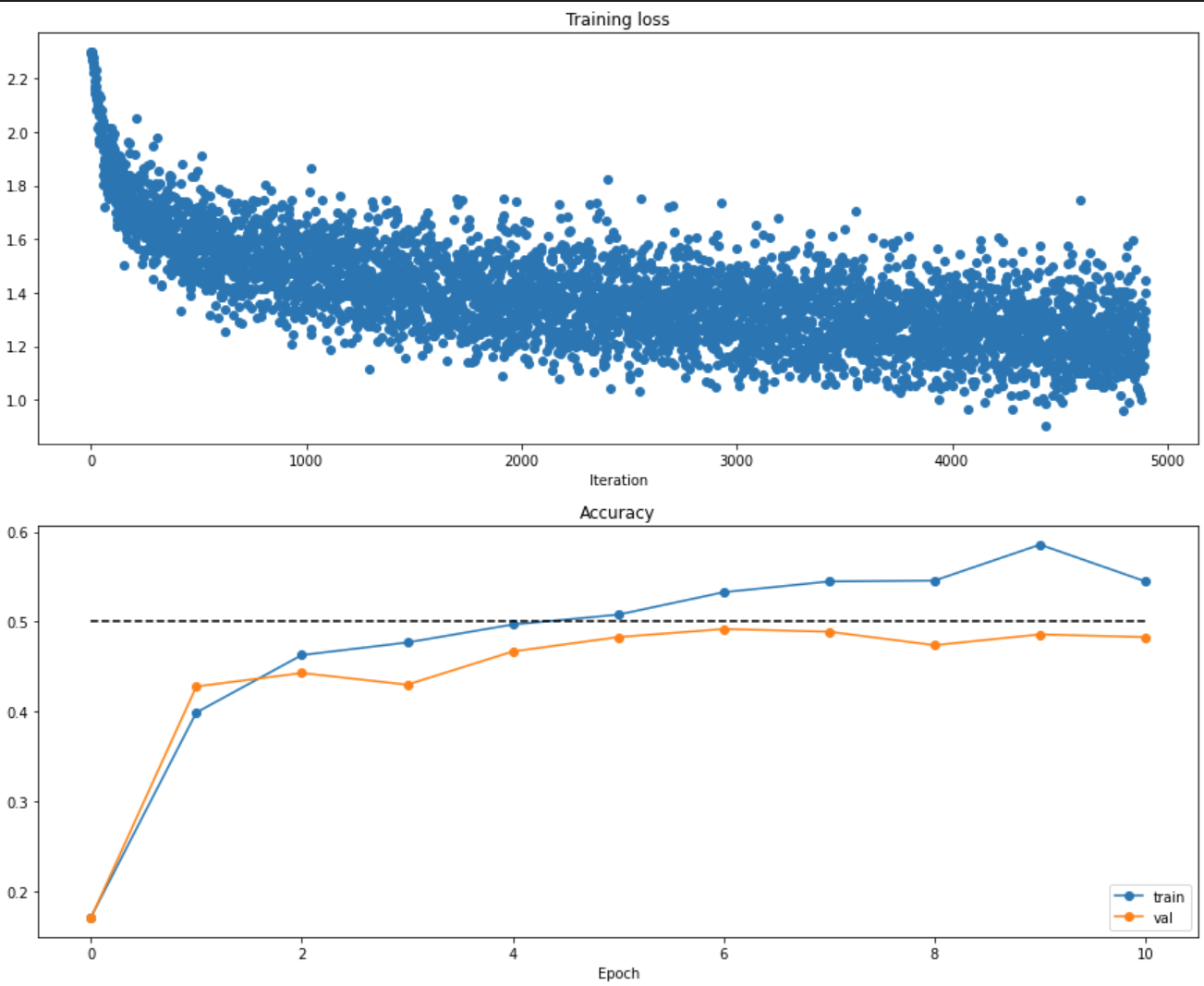
　　图标展示了不同轮次测试集上的准确率和验证集上的准确率，我们可以发现:随着我们迭代轮次（训练数据不断增多），损失函数成指数下降，同时，我们的训练数据的准确率也在不断上升，而至于为什么我们的训练集准确率仍大于测试集准确率，则是因为还是存在过拟合的现象，不过过拟合显然不是很严重，减小过拟合我们可以通过减少隐藏层的个数，增加训练数据，增大正则项等方法消除。值得注意的是，我们隐藏层决定了从输入层到隐藏层映射矩阵的规模，以及神经网络的学习能力，我们可以考虑，在人类的神经系统中，参与活动的神经元越多，显然这个活动越复杂，人类神经系统的神经元要多于其余生物，所以人类的学习能力就更强，因为有更多的节点可以用于处理信息；那么对于我们的前馈神经网络来说，学习能力过强就会导致过拟合，所以我们可以考虑适当减少隐藏层的节点个数，以防其过拟合。

　　同样，我们可以通过调整超参数来得到不同性能的分类器，我们可以考虑枚举法来得到最优超参数：

 1 best_model = None
 2 results={}
 3 best_val=-1
 4 learning_rates=[1e-7,1e-6,1e-5,1e-4]
 5 regularization_strengths = [1.5e4,2e4,5e4,0]
 6 hidden_sizes = [50,75,100]
 7 hyperparams=[(ls,rs,hid)for ls in learning_rates for rs in regularization_strengths for hid in hidden_sizes]
 8 for ls,rs,hid in hyperparams:
 9   model=TwoLayerNet(input_size,hid,num_classes,reg=rs)
10   solver=Solver(model,data,
11          update_rule='sgd',
12          optim_config={'learning_rate':ls,},
13          lr_decay=0.95,
14          num_epochs=10, batch_size=100,
15          print_every=100,
16          verbose=False)
17   solver.train()
18   train_acc=solver.train_acc_history[-1]
19   val_acc= solver.val_acc_history[-1]
20   if(val_acc>best_val):
21     best_val=val_acc
22     best_model=model
23   results[(ls,rs,hid)]=(train_acc,val_acc)
24 for ls,rs,hid in sorted(results):
25   train_accuracy, val_accuracy = results[(ls,rs,hid)]
26   print('lr %e reg %e hid %e train accuracy: %f val accuracy: %f' % (ls,rs,hid, train_accuracy, val_accuracy))
27
28 print('best validation accuracy achieved during cross-validation: %f' % best_val)
29 ########################################

change the params

　　我们可以得到如下的数据：

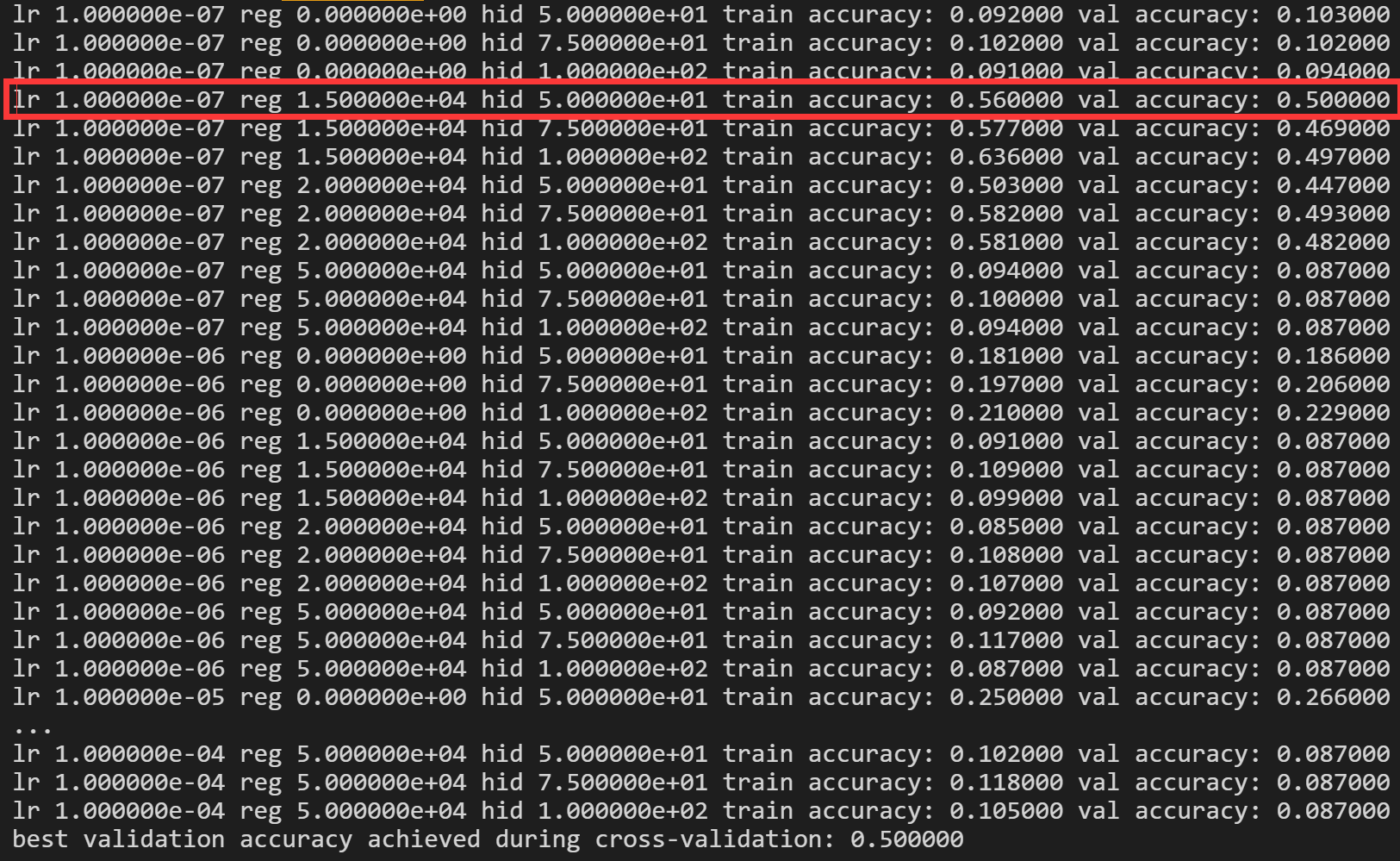
　　所以，我们的学习率在1e-7，正则项为1.5e4，隐藏层有50个节点，我们的模型在训练集上学习的水平最好。我们通过上面也可以看出：在其他参数相同的情况下，隐藏层越多，训练集的准确率越高，甚至有的分类器的性能可以在训练集上实现63.6%的准确率，可是在验证集上仅有49.7%的准确率，这便是过拟合，这与我们上面所述的结论也同样吻合。

　　之后，我们就可以用未知的测试集来测试我们模型的泛化能力了：

1 y_test_pred = np.argmax(best_model.loss(data['X_test']), axis=1)
2 print('Test set accuracy: ', (y_test_pred == data['y_test']).mean())

test

　　最终便能够得到我们的准确率，是50%左右。至此，两层全连接神经网络到此结束！

　　总结：在这里，我们实现了两层全连接神经网络，通过模块化调用的方法训练出了一个分类器，能够在测试集上达到50%左右的准确率；神经网络的基本模型是输入层-----隐藏层-----激活函数------输出层，在这里我们激活函数选取的是ReLU激活函数，然后两个映射的权重矩阵完全由Python随机出来，其服从期望为0，方差为weight_scale的标准正态分布，然后根据输入数据的轮次不断不断迭代我们的权重矩阵，最后得到一个相对比较合理的分类器。这便是神经网络最基础的结构，相较于SVM，我们增加了隐藏层，增强了分类器的学习能力，里面参与运算的超参数相应的也变多了，所带来的的结果就是模型的性能变强了，相应的，我们训练模型所需要的时间也更多了，可以说是各有利弊。总体而言，如果不输出一些中间变量以及损失函数等，我们的神经网络可能比现在要简单一些，至少代码的行数要少一些，不过我们应该侧重于理解神经网络的结构和功能，明白主体代码的实现思路，里面主要的算法全部是之前我们所描述过的，比如随机梯度下降，softmax损失函数等等。