08_N叉树的层序遍历

N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

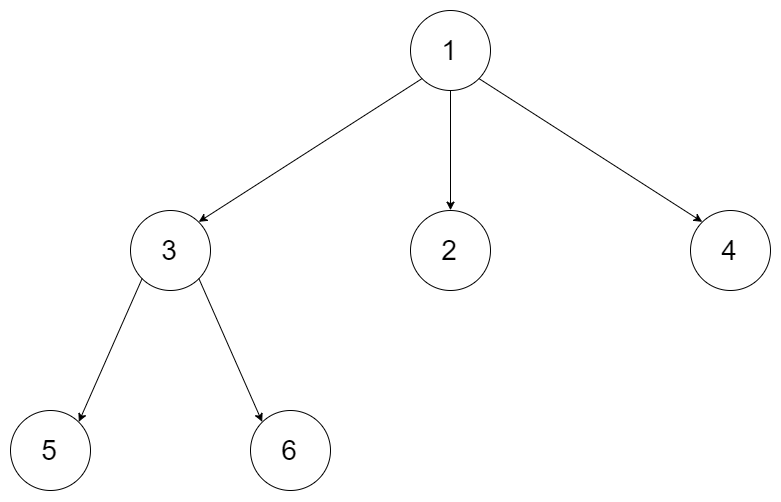
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

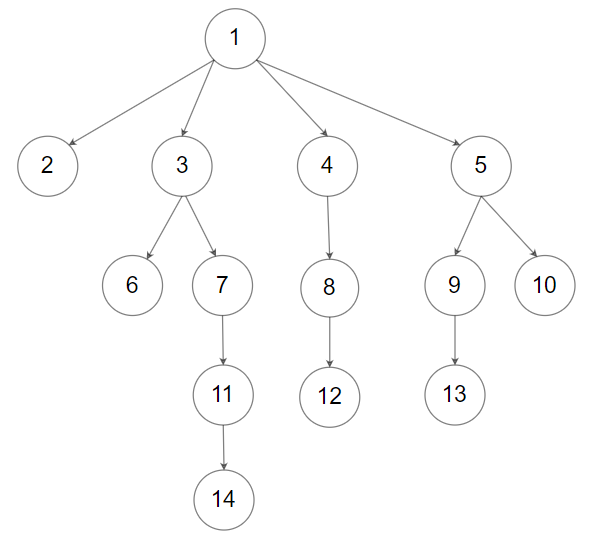
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

• 树的高度不会超过 1000
• 树的节点总数在 [0, 10^4] 之间

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        // 返回最终的结果列表
        List<List<Integer>> resList = new ArrayList<>();
        Queue<Node> que = new LinkedList<>();
        que.add(root);
        if (root == null) return resList;
        while (!que.isEmpty()) {
            // 统计队列中当前层所拥有的元素个数
            int levelSize = que.size();
            List<Integer> levelList = new ArrayList<>();
            for (int i = 0; i < levelSize; i++) {
                Node tmp = que.poll();
                levelList.add(tmp.val);
                List<Node> children = tmp.children;
                // 当前孩子结点为null或者长度为0，直接continue
                if (children == null || children.size() == 0) {
                    continue;
                }
                // 遍历当前节点的孩子节点，将其添加到队列中
                for (Node child: children) {
                    que.add(child);
                }
            }
            resList.add(levelList);
        }
        return resList;
    }
}