图解 LeetCode 算法汇总——回溯

本文首发公众号：小码A梦

回溯算法是一种常见的算法，常见用于解决排列组合、排列问题、搜索问题等算法，在一个搜索空间中寻找所有的可能的解。通过向分支不断尝试获取所有的解，然后找到合适的解，找完一个分支后再往回搜索。回溯算法通常使用递归的方式实现。

回溯本质是一种暴力搜索法，列出所有可能的解，然后找到合适的解。以 a、b、c的排列组合为例，画出全排列组合。

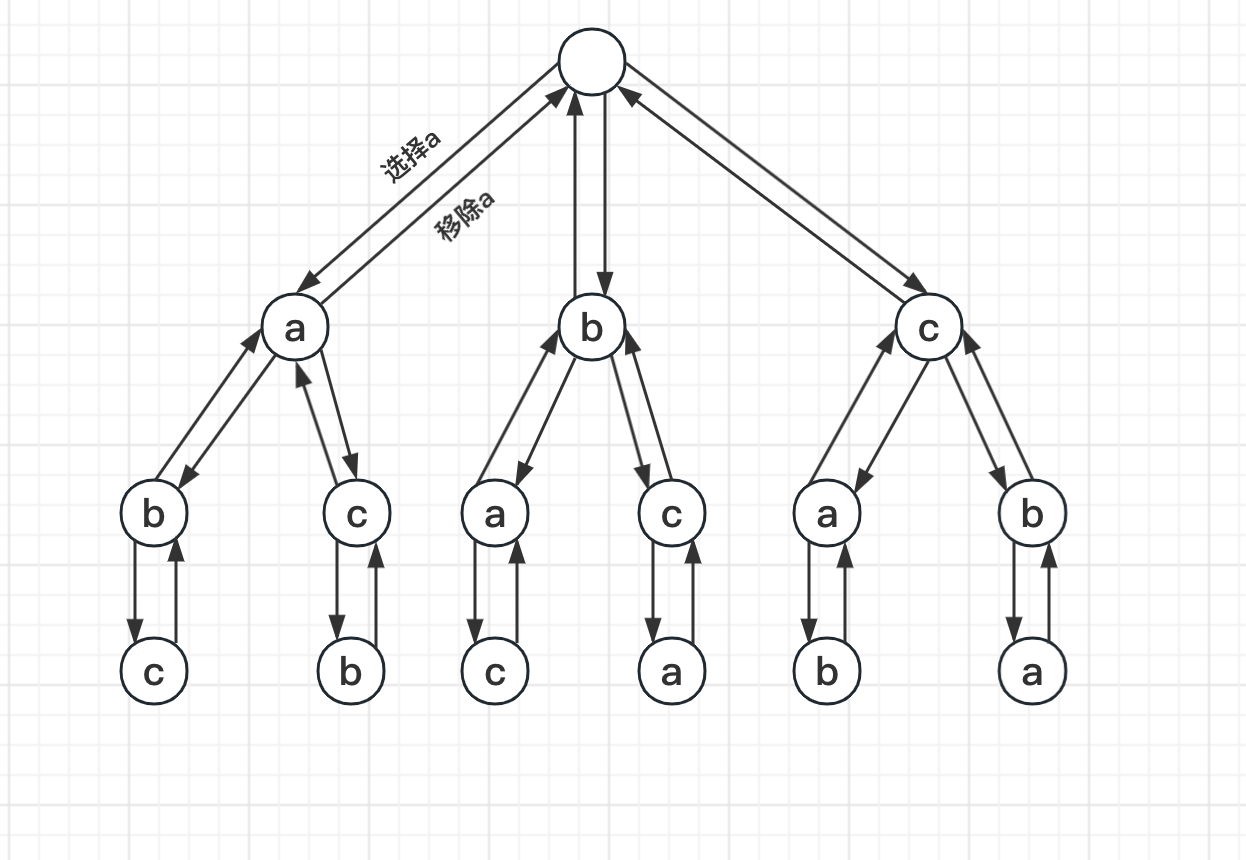
以上排列组合回溯步骤：

• 列出所有可能存在的组合。
• 分解组合，把问题分解多个阶段，每个阶段添加一个分叉。
• 走完一个分叉，或者遇到不符合期望条件的时，就退回到上一个分叉。继续走其它没走的路。直到走完所有的路。
• 回溯一半都是使用递归实现。

根据以上的步骤得出一个简单的回溯算法的模板：

public Solution {
   List<List<Integer>> result;

   LinkedList<Integer> path;

   //记录那些元素被遍历过
   boolean[] used;

   private List<List<Integer>> permute(int[] nums) {
        result = new ArrayList<>();
        path = new LinkedList<>();
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }

    private void permuteHelper(int[] nums) {
        if (递归终止条件) {
            result.add(new ArrayList<>(path));
            return;
        }
	    //遍历各个元素
        for (int i = 0; i < nums.length; i++) {
            used[i] = true;
	        //选择元素
            path.add(nums[i]);
            permuteHelper(nums);
	        //移除元素
            path.removeLast();
            used[i] = false;
        }
    }
}

以上代码使用递归，递归一般要设置一个终止条件，然后遍历整个元素，通过链表选择元素和移除元素。

LeetCode 题解

上面所说的，回溯主要解决一些排列组合、排列问题、搜索问题等问题，LeetCode 有很多类似的问题，这里选取了几个比较常见的题目。

• 39 组合总和
• 40 组合总和 II
• 46 全排列
• 47 全排列 II
• 51 N皇后

39.组合总和（中等）

题目描述

解法

这是一个比较典型的排列组合问题，本题采用的是求总和，使用总和减去遍历的数据，最后得到结果为零，就是符合的组合。

• 为了减少遍历次数，数组需要先排序。总数减的数据如果小于零，就不会在该分支继续遍历了。
• 可以重复使用元素，每次都遍历一遍全部元素。
• 减去分支结果之后，以新的结果，再创建分支做减法。
• 递归遍历一直到结果为零和负数。
  • 为零，符合条件，记录数据，对应的分支遍历终止，继续遍历下一个分支。
  • 为负数，返回到上一个分支，继续遍历后面的分支。

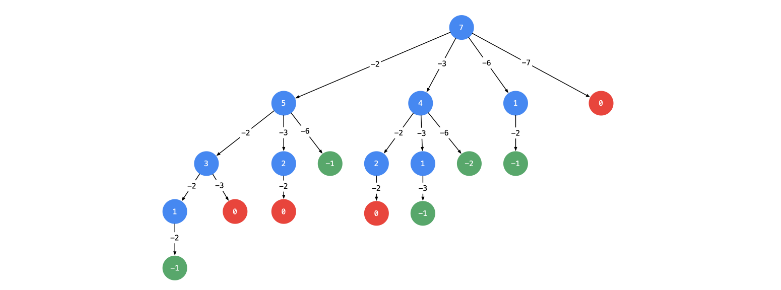
最终代码：

class Solution {

    List<List<Integer>> list = new ArrayList<>();

    int[] candidate;

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        Arrays.sort(candidates);
        candidate = candidates;
        recall(0,target,new LinkedList<>());
		return list;
    }

    private void recall(int start, int target, LinkedList<Integer> path) {
		if (target == 0) {
			list.add(new ArrayList<>(path));
			return;
		}
		for (int i = start; i <candidate.length ; i++) {
			int sub = target - candidate[i];
			if (sub < 0) {
				break;
			}
			path.add(candidate[i]);
			recall(i,sub,path);
			path.removeLast();
		}
	}
}

recall 使用递归方法遍历分支，而使用链表的特性，记录遍历的节点，如果不符合要求就上一个分支回撤，同时链表移除最后一个结点。

40.组合总和II（中等）

解题思路

这题的解题思路和上面的组合总和是差不多的，唯一不同的是元素不能被重复遍历，使用一个变量记录遍历的起始值，遍历过的数据，下次往后一位开始遍历。

代码如下：

class Solution {

    List<List<Integer>> list = new ArrayList<>();

	int[] candidate;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
		candidate = candidates;
		recall(0,target,new LinkedList<>());
		return list;
    }

    private void recall(int start, int target, LinkedList<Integer> path) {
	if (target == 0) {
		list.add(new ArrayList<>(path));
		return;
	}
	for (int i = start; i <candidate.length ; i++) {
	    //这里解决集合重复问题
		if (i > start && candidate[i] == candidate[i-1]) {
			continue;
		}
		int sub = target - candidate[i];
		if (sub < 0) {
			break;
		}
		path.add(candidate[i]);
		recall(i + 1,sub,path);
		path.removeLast();
	}
     }
}

start 记录遍历的起始值，其他解题方法和上面的组合求和是类似的。题目还有一个要求是不能出现重复的组合，就需要判断 candidate[i] == candidate[i-1] 就忽略该数据，往后继续遍历。

46.全排列

解题思路

• 每个元素都需要遍历一遍。
• 遍历元素的时，遍历完第一数，继续遍历未遍历的数据。
• 遍历结束后，返回上一个分叉。

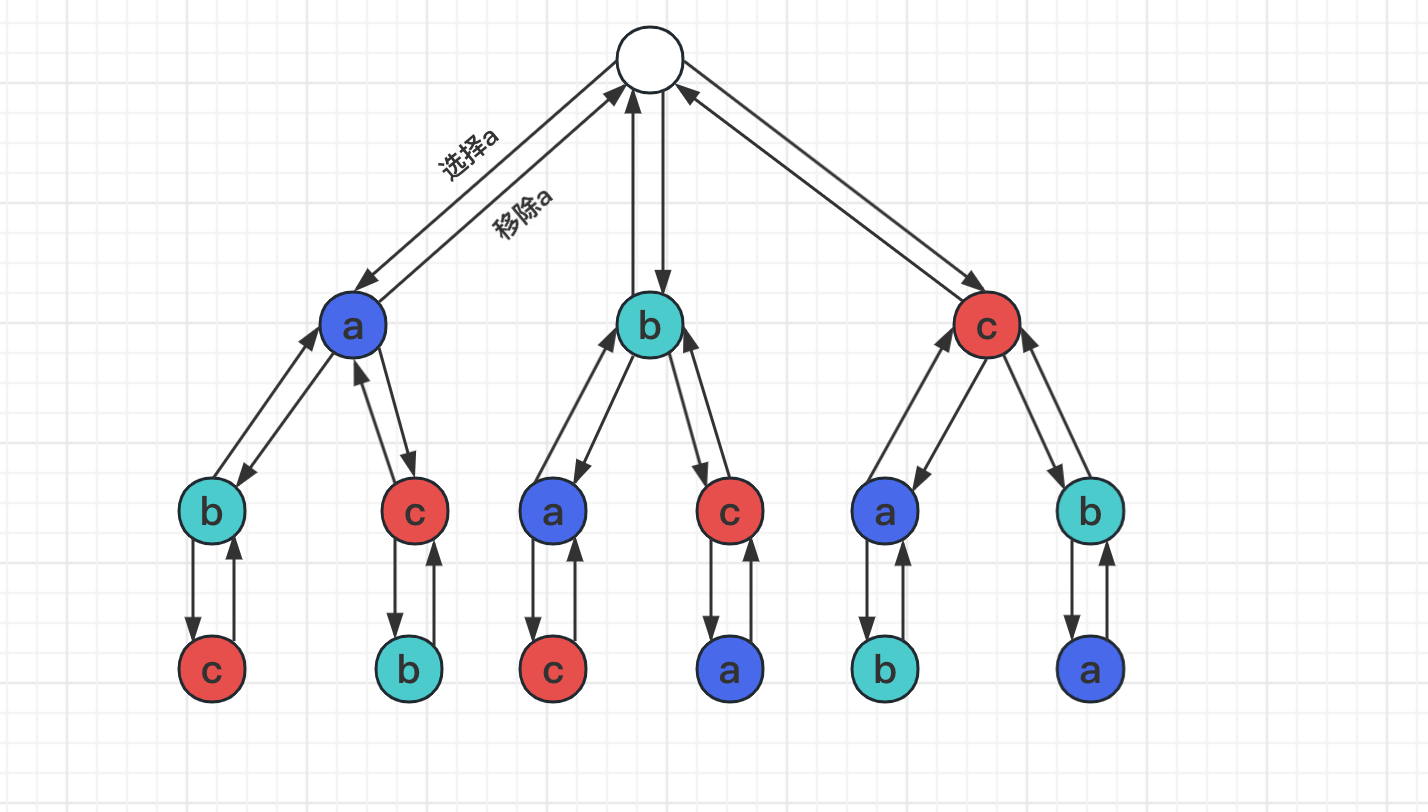
代码整理如下：

class Solution {
    List<List<Integer>> result = new ArrayList<>();

    LinkedList<Integer> path = new LinkedList<>();

    boolean[] used;

    public List<List<Integer>> permute(int[] nums) {
        if (nums.length == 0) {
            return result;
        }
        used = new boolean[nums.length];
        permuteHelper(nums);
        return result;
    }

    private void permuteHelper(int[] nums) {
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            permuteHelper(nums);
            path.removeLast();
            used[i] = false;
        }
    }
}

使用 used 记录哪些数据遍历过，遍历过的数据不会遍历，其他也是使用递归搜索。

51.N皇后

题目描述

解题思路

N 皇后问题是一个经典的回溯算法问题,是面试比较常见的问题。在一个 n * n 的棋盘上，每个格子放入的元素后，查看是够有同行、同列、左上方以及右上方是否冲突，冲突就回溯，不冲突就继续往下遍历。

• 初始化数组，默认初始值。
• 每一行只能放一个 Q,不冲突后，再遍历下一列的数据（因为同一行不能冲突）。
• 因为每一行只放一个 Q，所以不存在同行冲突。判断冲突就潘丹同一列、左上方以及右上方是否有冲突。
• 遍历到最后一行时，记录符合条件的数据。

class Solution {

    List<List<String>> res = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        // 初始化棋盘 "." 表示空，"Q"表示皇后，
		char[][] board = new char[n][n];
		for (char[] c : board) {
			Arrays.fill(c, '.');
		}
		backtrack(board, 0);
		return res;
    }

    private void backtrack(char[][] board, int row) {
		//终止条件
		if (row == board.length) {
			res.add(charToList(board));
			return;
		}
		//每一行列数(也就是长度)
		int n = board[row].length;
		for (int col = 0; col < n; col++) {
			//排除相互攻击的格子
			if (!isValid(board,row,col)) {
				continue;
			}
			//放入Q
			board[row][col] = 'Q';
			//进入下一行放皇后
			backtrack(board,row + 1);
			//撤销Q
			board[row][col] = '.';
		}
   }

   private boolean isValid(char[][] board, int row, int col) {
		int n = board.length;
		//检查列是否有皇后冲突
		for (int i = 0; i < n; i++) {
			if (board[i][col] == 'Q') {
				return false;
			}
		}
		//检查右上方是否有皇后冲突
		for (int i = row - 1,j = col + 1; i >= 0 && j < n; i--,j++) {
			if (board[i][j] == 'Q') {
				return false;
			}
		}
		//检查左上方是否有皇后冲突
		for (int i = row - 1,j = col - 1; i >= 0 && j >= 0; i--,j--) {
			if (board[i][j] == 'Q') {
				return false;
			}
		}
		return true;
	}

	public List<String> charToList(char[][] board) {
		List<String> list = new ArrayList<>();
		for (int i = 0; i < board.length; i++) {
			list.add(String.copyValueOf(board[i]));
		}
		return list;
	}
}

总结

回溯算法尝试在问题的解空间中搜索可能的解，并在搜索过程中进行选择、撤销选择和终止搜索，直到找到解或确定无解为止。

• 通常通过递归函数来实现回溯算法。
• 在每一步，需要做出选择（选择一个分支）然后递归地探索该选择的结果。
• 在递归返回后，需要撤销之前的选择，以便继续探索其他分支。
• 使用条件语句或循环来控制选择的范围和条件。