从MongoDB及mysql 谈B/B+树

一 B树的由来

B树指的是一类树，包括B-树，B+树，B*树等，是一种自平衡的搜索树，它类似普通的平衡二叉树，不同的一点是B树允许每个节点有更多的子节点。B树是专门为外部存储器设计的，如磁盘，它对于读取和写入大块数据有良好的性能，所以一般用在文件系统及数据库中。

1. 为什么不用二叉平衡树

传统用来搜索的平衡二叉树有很多，AVL树，红黑树等。这些树在一般情况下的查询性能非常好，但当数据量非常大的时候就无能为力了。数据量非常大时，内存不够用，大部分数据只能存放在磁盘上，只有需要的数据才加载到内存。一般而言内存的访问时间为50ns，而磁盘在10ms左右。速度相差了近5个数量级，程序大部分的时间阻塞在磁盘IO上。所以核心就是要减少磁盘IO次数。而像AVL树，红黑树这类平衡二叉树从设计上无法"迎合"磁盘。

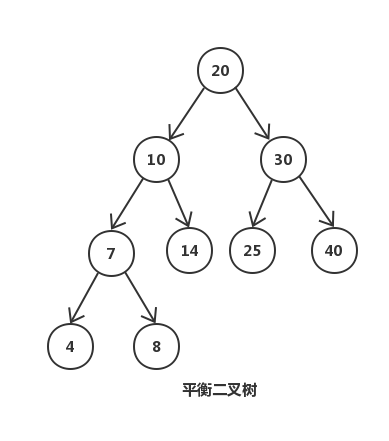
上图是一颗简单的平衡二叉树，我们来看下为什么数据库和文件系统用b树而不用平衡二叉树:

(1) 它的平衡是通过旋转来实现的，而旋转是对整个树的操作，若部分加载到内存中则无法完成旋转操作。

(2) 平衡二叉树的高度比较大(log n), 这样逻辑上很近的节点实际可能非常远，无法很好地利用磁盘预读（空间的局部性原理）

2. 从"迎合"磁盘的角度来看看B树的设计

索引的效率实际上依赖于磁盘IO的次数，加快索引的办法就是有效地减少磁盘IO次数。相比于平衡二叉树每次将范围分割为两个区间，B树每次将范围分割成多个区间，区间越多，定位数据越快越精确。多叉降低了B树的高度(底数很大的log n，二叉是底数为2). 那么节点为区间范围，每个节点就比较大了。因此新建节点时，直接申请页大小的空间(磁盘时按照block分的，一般为512 byte。磁盘IO一次读取若干个block，我们称为一页，具体大小和操作系统有关，一般为4k，8k或16k)，计算机内存分配是按页对齐的，这样一个节点只需要一次IO。那么多叉树的总IO次数也就缩减为log n次。

二 B-树

1. B-树的结构

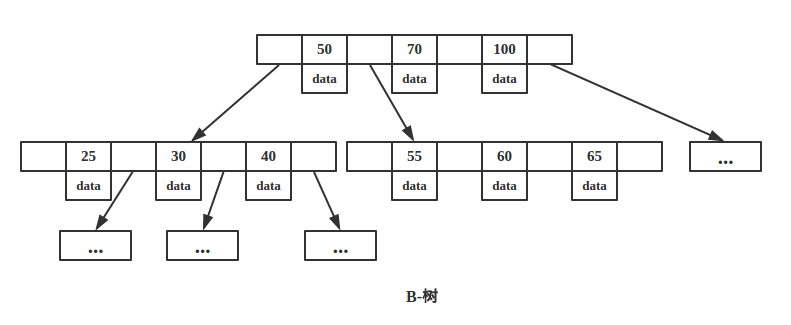
上面是一颗B-树，B-树的插入和删除就不具体介绍了，很多资料都描述了这一过程。在普通平衡二叉树中，插入删除后若不满足平衡条件则进行旋转操作，而在B-树中，插入删除后不满足条件则进行分裂及合并操作。

2. B-树的查找

我们来看看B-树的查找，假设每个节点有 n 个 key值，被分割为 n+1 个区间，注意，每个 key 值紧跟着 data 域，这说明B-树的 key 和 data 是聚合在一起的。一般而言，根节点都在内存中，B-树以每个节点为一次磁盘 IO，比如上图中，若搜索 key 为 25 节点的 data，首先在根节点进行二分查找（因为 keys 有序，二分最快），判断 key 25 小于 key 50，所以定位到最左侧的节点，此时进行一次磁盘 IO，将该节点从磁盘读入内存，接着继续进行上述过程，直到找到该 key 为止。

三 B+树

1. B+树的结构

B+树是B-树的变种，它与B-树的不同之处在于：

在B+树中，key 的副本存储在内部节点，真正的 key 和 data 存储在叶子节点上 。
n 个 key 值的节点指针域为 n 而不是 n+1。

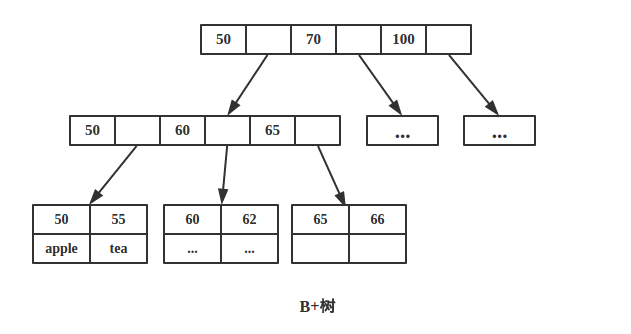
因为内节点并不存储 data，所以一般B+树的叶节点和内节点大小不同，而B-树的每个节点大小一般是相同的，为一页。

为了增加 区间访问性，一般会对B+树做一些优化。
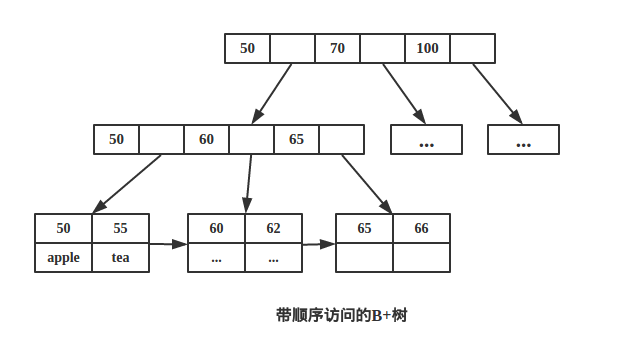
如下图带顺序访问的B+树。

三 B-树和B+树的区别

1. 时间复杂度

B+树节点不存储数据，所有data存储在叶节点导致查询时间负责度固定为log n。而B-树查询时间复杂度不固定，与key在树中的位置有关，最好为O(1)

下面为图示:

B-树

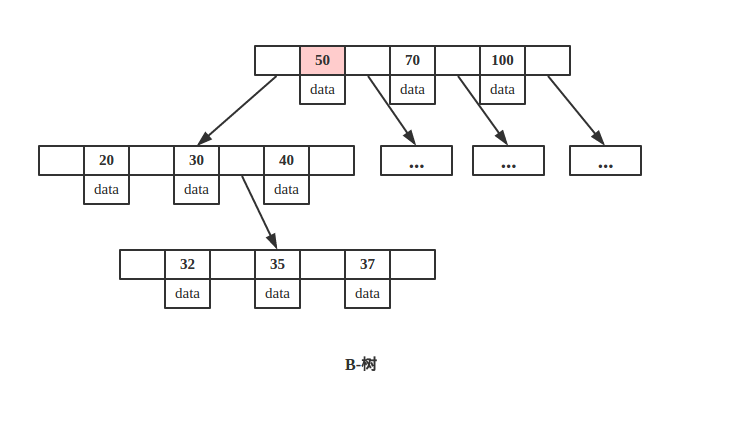
从上图可以看出，key 为 50 的节点就在第一层，B-树只需要一次磁盘 IO 即可完成查找。所以说B-树的查询最好时间复杂度是 O(1)。

B+树

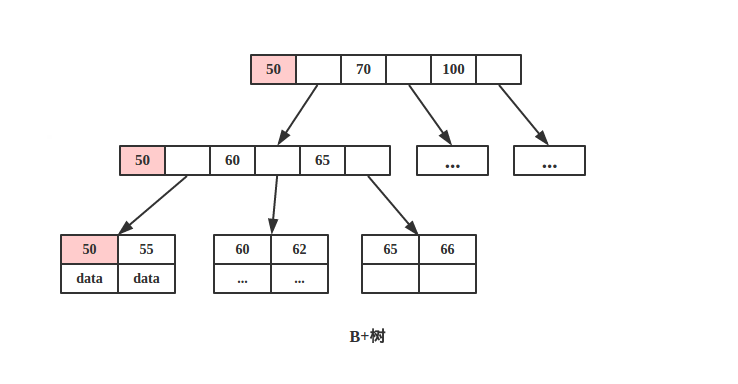
由于B+树所有的 data 域都在根节点，所以查询 key 为 50的节点必须从根节点索引到叶节点，时间复杂度固定为 O(log n)。

2. 区间查找

B+树叶节点两两相连可大大增加区间访问性，可使用在范围查询等，而B-树每个节点key 和data在一起，则无法区间查找

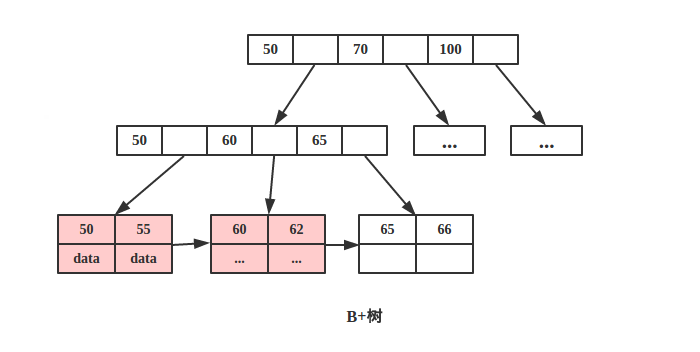
B+树可以很好的利用局部性原理，若我们访问节点 key为 50，则 key 为 55、60、62 的节点将来也可能被访问，我们可以利用磁盘预读原理提前将这些数据读入内存，减少了磁盘 IO 的次数。
当然B+树也能够很好的完成范围查询。比如查询 key 值在 50-70 之间的节点。

3. B+树更适合外部存储。由于内节点无 data 域，每个节点能索引的范围更大更精确

这个很好理解，由于B-树节点内部每个 key 都带着 data 域，而B+树节点只存储 key 的副本，真实的 key 和 data 域都在叶子节点存储。前面说过磁盘是分 block 的，一次磁盘 IO 会读取若干个 block，具体和操作系统有关，那么由于磁盘 IO 数据大小是固定的，在一次 IO 中，单个元素越小，量就越大。这就意味着B+树单次磁盘 IO 的信息量大于B-树，从这点来看B+树相对B-树磁盘 IO 次数少。

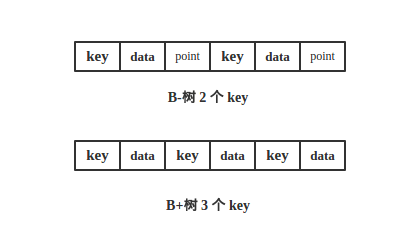
从上图可以看出相同大小的区域，B-树仅有 2 个 key，而B+树有 3 个 key。

三为什么MongoDB索引选择B-树，而mysql索引选择B+树

1 mysql 和 MongoDB

mysql是传统的关系型数据库，而MongoDB是文档形的数据库，是一种nosql，它使用xml或json格式来保存数据，归属于聚合型数据库。（键值数据库也属于聚合型数据库，比如redis）

2 例子