【leetcode】【二分 | 牛顿迭代法】69_Sqrt(x)

题目链接：传送门

题目描述：

　　求Sqrt(x),返回整数值即可。

【代码】：

 #include<bits/stdc++.h>
 using namespace std;
 const int N = 1e6+ ;
 /*
 int mySqrt ( int x ){
     int L = 1 , R = N , mid , ans = 0 ;
     while ( L <= R ){
         mid = ( L + R ) >> 1 ;
         if( mid <= x / mid ){
             L = mid + 1 ;
             ans = mid ;
         }else {
             R = mid - 1 ;
         }
     }
     return ans ;
 }
 */
 int mySqrt ( int x ) {
     if ( !x )
         return  ;
     double eps = 1e-;
     double res = x , Last;
     while ( true ){
         Last = res ;
         res = 0.5 * ( res + x/res ) ;
         if( fabs( Last - res ) < eps){
             break ;
         }
     }
     return (int)res;
 }
 int main()
 {
     int n;
     while ( ~scanf("%d",&n) ) {
         printf(" Sqrt (%d) = %d \n",n,mySqrt(n) );
     }
     return ;
 }

mySqrt

【题解】：

　　首先有两个做法。

　　第一个就是二分法，大家要记住，这个方法需要判溢出，不然会一直错。需要“移乘变除”

　　第二种方法就是我想写博客来记录的，我觉得真的非常好的一个想法，就是“牛顿迭代法”。

　　　　　　主要参考博客和网站：1、求牛顿开方法的算法及其原理，此算法能开任意次方吗?

　　　　　　　　　　　　　　　　2、如何通俗易懂地讲解牛顿迭代法？

　　　　　　　　　　　　　　　　3、知乎“如何通俗易懂地讲解牛顿迭代法求开方？数值分析？”

　　以下就是知乎一些比较出色的解答

　　“黄徐升”的回答：

　　

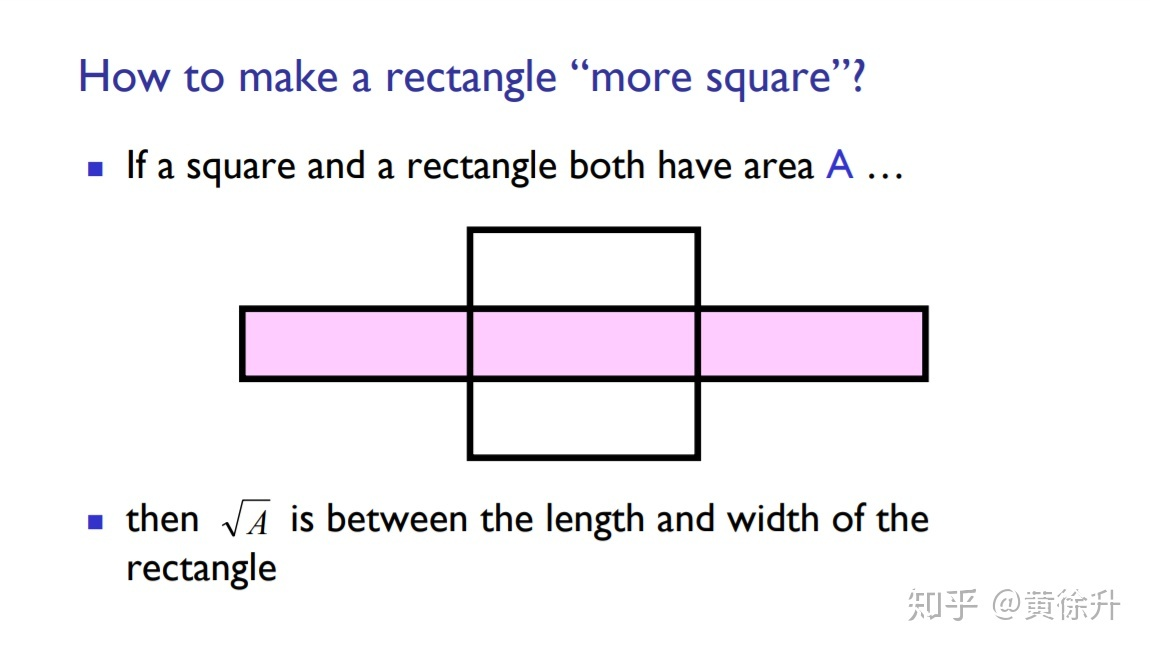
　　有一个利用“将长方形变得更像正方形”的思路也可以得到求 的算数平方根的迭代公式

　　算是通俗易懂地得到了这个迭代公式（不过并没有体现牛顿法的求导等过程，那个用抛物线的切线看是比较直观的，别的回答里已经有了）。

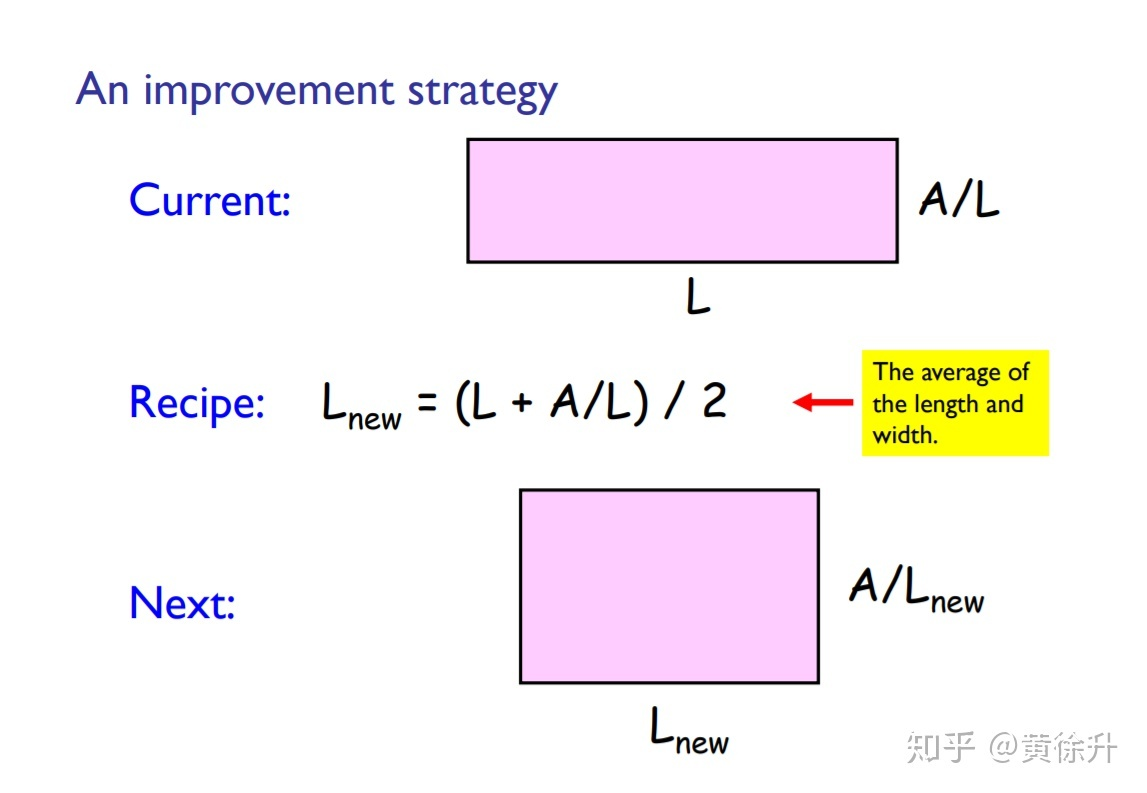
首先是考虑 是面积为 的正方形的边长，如果画一个邻边不等的面积是 长方形，设这个长方形的长为 ，宽为 ，那么怎样能让这个长方形变得更像一个正方形呢？是要把长变得短一点，宽变得长一点，可以用长和宽的平均数 来作为新的长 ，在面积不变的条件下，新的宽是 。这样不断操作下去，长方形的长和宽会越来越接近，就是一直趋近与 了。

　　

---

【牛顿迭代法】

假设方程 在  附近有一个根，那么用以下迭代式子：
 
依次计算、、、……，那么序列将无限逼近方程的根。

牛顿迭代法的原理很简单，其实是根据f(x)在x0附近的值和斜率，估计f(x)和x轴的交点，看下面的动态图：

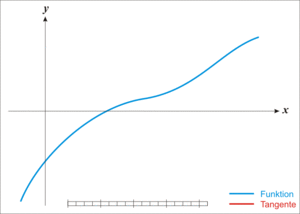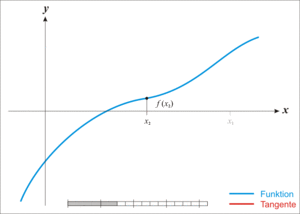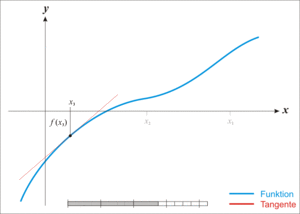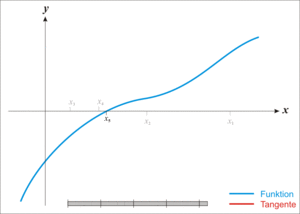
【用牛顿迭代法开平方】

令：
 
所以f(x)的一次导是：

牛顿迭代式：

随便一个迭代的初始值，例如，代入上面的式子迭代。

例如计算，即a=2。



……

计算器上可给出

【用牛顿迭代法开任意次方】

求的递推式是：