kmp算法分析和C++实现

知乎高赞分析

作者：逍遥行

链接：https://www.zhihu.com/question/21923021/answer/37475572
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

角色：

甲：abbaabbaaba
乙：abbaaba

乙对甲说：「帮忙找一下我在你的哪个位置。」

甲从头开始与乙一一比较，发现第 7 个字符不匹配。

要是在往常，甲会回退到自己的第 2 个字符，乙则回退到自己的开头，然后两人开始重新比较。这样的事情在字符串王国中每天都在上演：不匹配，回退，不匹配，回退，……

但总有一些妖艳字符串要花出自己不少的时间。

上了年纪的甲想做出一些改变。于是甲把乙叫走了：「你先一边玩去，我自己研究下。」

甲给自己定了个小目标：发生不匹配，自己不回退。

甲发现，若要成功与乙匹配，必须要匹配 7 个字符。也就是说，就算自己回退了，在后续的匹配流程中，肯定还要匹配自己的第 7 个字符。

当在甲的某个字符 c 上发生不匹配时，甲即使回退，最终还是会重新匹配到字符 c 上。

那干脆不回退，岂不美哉！

甲不回退，乙必须回退地尽可能少，并且乙回退位置的前面那段已经和甲匹配，这样甲才能不用回退。

如何找到乙回退的位置？

「不匹配发生时，前面匹配的那一小段 abbaab 于我俩是相同的」，甲想，「这样的话，用 abbaab 的头部去匹配 abbaab 的尾部，最长的那段就是答案。」

具体来说，
abbaab 的头部有 a, ab, abb, abba, abbaa（不包含最后一个字符。下文称之为「前缀」）
abbaab 的尾部有 b, ab, aab, baab, bbaab（不包含第一个字符。下文称之为「后缀」）
这样最长匹配是 ab，乙回退到第三个字符和甲继续匹配。

「要计算的内容只和乙有关」，甲想，「那就假设乙在所有位置上都发生了不匹配，乙在和我匹配之前把所有位置的最长匹配都算出来（算个长度就行），生成一张表，之后我俩发生不匹配时直接查这张表就行。」

据此，甲总结出了一条甲方规则：

所有要与甲匹配的字符串，必须先自身匹配：对每个子字符串 [0...i]，算出其「相匹配的前缀与后缀中，最长的字符串的长度」。

甲把乙叫了回来，告诉他新出炉的甲方规则。

「小 case，我对自己还不了解吗」，乙眨了一下眼睛，「那我回退到第三个字符和你继续匹配就行了」。

原理分析

在所有字符串匹配算法里最知名的一种非kmp算法莫属，很多时候提到字符串匹配我们首先想到的就是kmp算法。但kmp算法是出了名的不好懂，个人也是一直理解不好。而上面知乎高赞的分析我觉得用来理解KMP算法非常形象，对于理解kmp算法的核心原理非常有帮助。

简单总结上面的分析：在模式串和主串匹配过程中，当遇到坏字符后，主串不回退，用已经匹配的字符串的头部匹配其尾部，即前缀匹配后缀，直接回退到最长匹配前缀的尾部位置。

很明显，已匹配的字符串其实就是模式串的一部分，所以如何计算已匹配的字符串的最长匹配，其实可以不涉及主串。而模式串每一部分的最长匹配前缀的尾部位置其实预先计算好，在模式串和主串匹配的过程中直接拿过来用就好。kmp算法就是提前构建一个数组，用来存储模式串中每个前缀的最长可匹配前缀子串的结尾字符的下标。我们把这个数组定义为next数组，很多书还为这个数组起了一个名字叫失效数组（failure function）。

数组的下标是每个前缀结尾字符下标，数组的值是这个前缀的最长可匹配前缀子串的结尾字符的下标。这句话比较难理解，看下面是极客时间王争专栏的例子就应该一看就懂了。

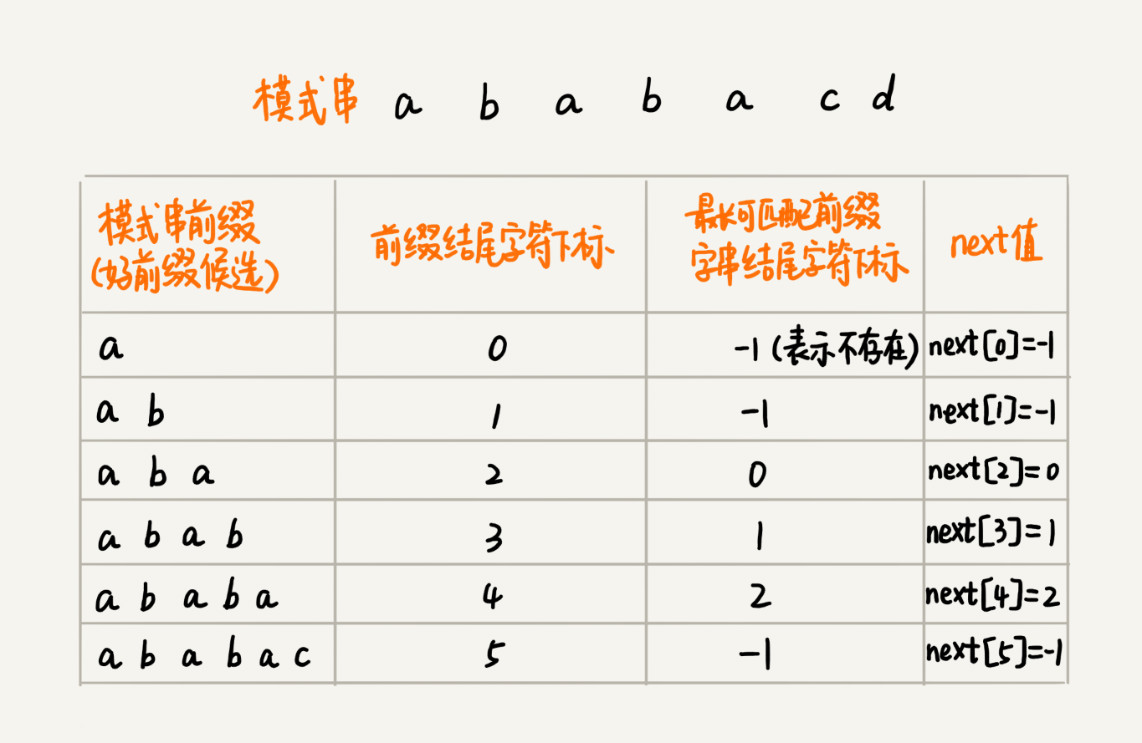
至此，我觉得已经足够从原理上理解kmp算法了，具体实现的细节下面的的C++代码实现已经足够清楚，此处不再赘述。本人理解kmp算法过程非常坎坷，之前自以为理解了其实根本没弄懂，写的博文纯粹也是误人子弟，所以现在重新修改后有种如释重负的感觉。这里，再次感谢知乎的回答的作者和王争老师帮助！

代码实现

#ifndef _KMP_H
#define _KMP_H

#include <string>
#include <vector>
#include <list>

std::vector<int> getNext(std::string &s) {
    int k = -;
    int i = ;
    std::vector<int> next(s.size(), -);
    for (int i = ; i < s.size(); ++i) {
        while (k != - && s[k + ] != s[i]) {
            k = next[k];
        }
        if (s[k + ] == s[i]) {
            ++k;
        }
        next[i] = k;
    }
    return next;
}

std::list<int> kmp(std::string &text, std::string &s) {
    std::list<int> posList;
    std::vector<int> next = getNext(s);
    int k = -;
    for (int i = ; i < text.size(); ++i) {
        while (k != - && s[k + ] != text[i]) {
            k = next[k];
        }
        if (s[k + ] == text[i]) {
            k++;
        }
        if (k == s.size() - ) {
            posList.push_back(i - k);
            k = next[k];
        }
    }
    return posList;
}

#endif