常用算法

>>>1. 顺序查找, 也叫线性查找, 它从第一个记录开始, 挨个进行对比, 是最基本的查找技术

javaScript 版顺序查找算法:

  1.  // 顺序查找(线性查找) 只做找到即返回
  2.  
  3.  // javaScript 版
  4.  
  5.  function search(data,needle)
  6.  
  7.  {
  8.  
  9.      for(var i=0;i<data.length;i++)
  10.  
  11.      {
  12.  
  13.          if(data[i] == needle && typeof data[i] == typeof needle)
  14.  
  15.          {
  16.  
  17.              return i;
  18.  
  19.          }
  20.  
  21.      }
  22.  
  23.      return false;
  24.  
  25.  }
  26.  
  27.  var data = [100,10,2,7,8,6];
  28.  
  29.  console.log(search(data,7));//
  30.  
  31.  console.log(search(data,'7'));// false

php版顺序查找算法:

  1.  <?php
  2.  
  3.  // php版
  4.  
  5.  function search($data,$needle)
  6.  
  7.  {
  8.  
  9.      $data_len = count($data);
  10.  
  11.      for($i=0;$i<$data_len;$i++)
  12.  
  13.      {
  14.  
  15.          if($data[$i] === $needle) return $i;
  16.  
  17.      }
  18.  
  19.      return false;
  20.  
  21.  }
  22.  
  23.  $data = [100,10,2,7,8,6];
  24.  
  25.  var_dump(search($data,7));// int(3)
  26.  
  27.  var_dump(search($data,'7'));// bool(false)

python3 版顺序查找算法:

  1.  # python3 版本
  2.  
  3.  def search(data,needle) :
  4.  
  5.      dataLen = len(data)
  6.  
  7.      for i in range(dataLen) :
  8.  
  9.          if data[i] == needle and type(data[i]) == type(needle) : return i
  10.  
  11.      return False
  12.  
  13.  data = [100,10,2,7,8,6]
  14.  
  15.  print(search(data,7))   #
  16.  
  17.  print(search(data,'')) # False
  18.  
  19.  print(search(data,6))   #

>>>二分找查, 折半查找

核心思想:

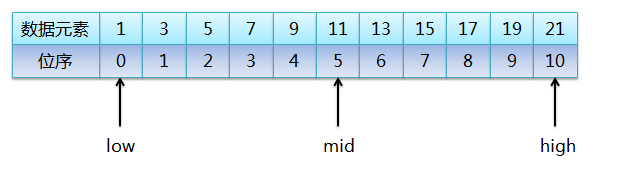
1. 用low , high , middle 表示待查找区间的 下界, 上界,中间 的坐标

2. 取中间位置 middle = floor((low+high)/2)

3. 用给定值与 中间位置的值 作比较

等于: 查找成功

大于: 待查数据在区间的后半段  设low 为 middle+1

小于: 待查数据在区间的前半段  设high 为 middle-1

4.数据是排序好的

5.直到越界 (low>high) 查找失败, 结束

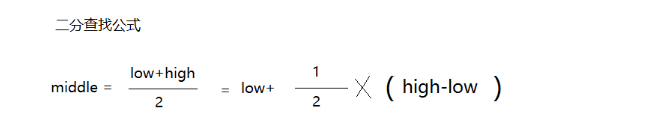
PHP版二分查找算法:

  1.  <?php
  2.  
  3.  // 二分法 折半查找 PHP版
  4.  
  5.  $data_list = [1,2,4,5,5,6,10,12];
  6.  
  7.  function bisearch($data_list,$needle)
  8.  
  9.  {
  10.  
  11.      $low = 0;
  12.  
  13.      $high = count($data_list)-1;
  14.  
  15.      if($data_list[$low] == $needle) return $low;
  16.  
  17.      if($data_list[$high] == $needle) return $high;
  18.  
  19.      while($high>=$low)
  20.  
  21.      {
  22.  
  23.          $middle = floor(($low+$high)/2);
  24.  
  25.          if($needle == $data_list[$middle])
  26.  
  27.          {
  28.  
  29.              return $middle;
  30.  
  31.          }elseif($needle>$data_list[$middle])
  32.  
  33.          {
  34.  
  35.              $low = $middle+1;
  36.  
  37.          }else{
  38.  
  39.              $high = $middle-1;
  40.  
  41.          }
  42.  
  43.      }
  44.  
  45.      return false;
  46.  
  47.  }
  48.  
  49.  print_r(bisearch($data_list,10)); //
  50.  
  51.  print_r(bisearch($data_list,5));  //
  52.  
  53.  print_r(bisearch($data_list,13)); // false

python 3版 二分查找算法:

  1.  import math
  2.  
  3.  # python3 版二分查找算法
  4.  
  5.  def bisearch(data_list,needle) :
  6.  
  7.      low,high = 0,len(data_list)-1
  8.  
  9.      if needle == data_list[low] :  return low
  10.  
  11.      if needle == data_list[high] : return high
  12.  
  13.      while high>=low :
  14.  
  15.          middle = math.floor((high+low)/2)
  16.  
  17.          if needle == data_list[middle] :  return middle
  18.  
  19.          elif needle > data_list[middle] : low = middle+1
  20.  
  21.          else : high = middle-1
  22.  
  23.      return False
  24.  
  25.  data_list = [1,2,4,5,5,6,10,12]
  26.  
  27.  print(bisearch(data_list,10));   #
  28.  
  29.  print(bisearch(data_list,5));    #
  30.  
  31.  print(bisearch(data_list,13));   # False

javaScript 版二分查找算法:

  1.  // js 版二分查找
  2.  
  3.  function bisearch(data_list,needle)
  4.  
  5.  {
  6.  
  7.      var low = 0,high = data_list.length-1
  8.  
  9.      if (needle == data_list[low] ) return low
  10.  
  11.      if (needle == data_list[high]) return high
  12.  
  13.      while (high>=low)
  14.  
  15.      {
  16.  
  17.          var middle = Math.floor((low+high)/2)
  18.  
  19.          if(needle == data_list[middle])
  20.  
  21.          {
  22.  
  23.              return middle
  24.  
  25.          }else if(needle>data_list[middle])
  26.  
  27.          {
  28.  
  29.              low = middle + 1
  30.  
  31.          }else{
  32.  
  33.              high = middle - 1
  34.  
  35.          }
  36.  
  37.      }
  38.  
  39.      return false
  40.  
  41.  }
  42.  
  43.  data_list = [1,2,4,5,5,6,10,12]
  44.  
  45.  console.log(bisearch(data_list,10));   //
  46.  
  47.  console.log(bisearch(data_list,5));    //
  48.  
  49.  console.log(bisearch(data_list,13));   // False

>>> 插值查找 (由二分查找改进)

二分查找的公式:

middle = (low+high)/2    => low+(1/2)*(high-low)

插值查找的公式由上面演变, 主要改进的是二分之一部分:

middle = low+((needle-data[low])/(data[high]-data[low]))*(high-low)

对二分查找跟插值查找的一个说明:

插值查找对于公布均匀的数据, 速度比二分查找快(插值查找次数少),例如对下面这类数据

$data = [1,2,3,6,7,9,10,11,...]

对于分布不均匀的数据, 二分查找要比插值查找快 例如下:

$data = [4,100,300,685,3452,...]

PHP版 插值查找算法:

  1.  <?php
  2.  
  3.  // 二分查找优化(插值查找) PHP版
  4.  
  5.  $data_list = [1,2,4,5,5,6,10,12];
  6.  
  7.  function interpolation($data_list,$needle)
  8.  
  9.  {
  10.  
  11.      $low = 0;
  12.  
  13.      $high = count($data_list)-1;
  14.  
  15.      if($data_list[$low] == $needle) return $low;
  16.  
  17.      if($data_list[$high] == $needle) return $high;
  18.  
  19.      while($high>=$low)
  20.  
  21.      {
  22.  
  23.          $middle = floor($low+(($needle-$data_list[$low])/($data_list[$high]-$data_list[$low]))*($high-$low));
  24.  
  25.          if($needle == $data_list[$middle])
  26.  
  27.          {
  28.  
  29.              return $middle;
  30.  
  31.          }elseif($needle>$data_list[$middle])
  32.  
  33.          {
  34.  
  35.              $low = $middle+1;
  36.  
  37.          }else{
  38.  
  39.              $high = $middle-1;
  40.  
  41.          }
  42.  
  43.      }
  44.  
  45.      return false;
  46.  
  47.  }
  48.  
  49.  print(interpolation($data_list,10)); //
  50.  
  51.  print(interpolation($data_list,5));  //
  52.  
  53.  print(interpolation($data_list,13)); // false
  54.  
  55.  $index = interpolation($data_list,10);
  56.  
  57.  echo $data_list[$index];//
  58.  
  59.  /*
  60.  
  61.   注: 1.floor 返回的是浮点数 如 6 类型为float
  62.  
  63.       2.false 用print,echo 输出是空字符串
  64.  
  65.  */

python3版 插值查找算法:

  1.  import math
  2.  
  3.  # python3 插值查找算法
  4.  
  5.  def interpolation(data_list,needle) :
  6.  
  7.      low,high = 0,len(data_list)-1
  8.  
  9.      if needle == data_list[low] :  return low
  10.  
  11.      if needle == data_list[high] : return high
  12.  
  13.      while high>=low :
  14.  
  15.          middle = math.floor(
  16.  
  17.              low+
  18.  
  19.              ((needle-data_list[low])/(data_list[high]-data_list[low]))*
  20.  
  21.              (high-low)
  22.  
  23.          )
  24.  
  25.          if needle == data_list[middle] :  return middle
  26.  
  27.          elif needle > data_list[middle] : low = middle+1
  28.  
  29.          else : high = middle-1
  30.  
  31.      return False
  32.  
  33.  data_list = [1,2,4,5,5,6,10,12]
  34.  
  35.  print(interpolation(data_list,10));   #
  36.  
  37.  print(interpolation(data_list,5));    #
  38.  
  39.  print(interpolation(data_list,13));   # False

js 版插值查找算法:

  1.  // js版 插值查找算法
  2.  
  3.  function interpolation(data_list,needle)
  4.  
  5.  {
  6.  
  7.      var low = 0,high = data_list.length-1
  8.  
  9.      if (needle == data_list[low] ) return low
  10.  
  11.      if (needle == data_list[high]) return high
  12.  
  13.      while (high>=low)
  14.  
  15.      {
  16.  
  17.          var middle = Math.floor(
  18.  
  19.              low+((needle-data_list[low])/(data_list[high]-data_list[low]))*
  20.  
  21.              (high-low)   
  22.  
  23.          )
  24.  
  25.          if(needle == data_list[middle])
  26.  
  27.          {
  28.  
  29.              return middle
  30.  
  31.          }else if(needle>data_list[middle])
  32.  
  33.          {
  34.  
  35.              low = middle + 1
  36.  
  37.          }else{
  38.  
  39.              high = middle - 1
  40.  
  41.          }
  42.  
  43.      }
  44.  
  45.      return false
  46.  
  47.  }
  48.  
  49.  data_list = [1,2,4,5,5,6,10,12]
  50.  
  51.  console.log(interpolation(data_list,10));   //
  52.  
  53.  console.log(interpolation(data_list,5));    //
  54.  
  55.  console.log(interpolation(data_list,13));   // False

小结:

以上有php,python,js 版常见的查找算法:

1. 顺序(线性) 查找

2. 二分查找 (折半查找)

3. 插值查找 (二分查找优化 适用于分布均匀的数据)

4. 前提是数据排好序, 顺序

常见查找算法之php, js,python版的更多相关文章

  1. 常见排序算法原理及JS代码实现

    目录 数组 sort() 方法 冒泡排序 选择排序 插入排序 希尔排序 归并排序 堆排序 快速排序 创建时间:2020-08-07 本文只是将作者学习的过程以及算法理解进行简单的分享,提供多一个角度的 ...

  2. 常见查找算法（Java代码实现）

    一,顺序查找 查找算法中顺序查找算是最简单的了,无论是有序的还是无序的都可以,只需要一个个对比即可,但其实效率很低.我们来看下代码 public static int search(int[] a, ...

  3. 排序算法（C语言+Python版）宝宝再也不怕面试官写排序算法了

    直接插入排序 过程: 1. 数据可分看成两个部分,前面的数据是有序的 2. 从后面的数据取出一个元素,插到前面有序数据的合适位置 从右端开始查找,到找到比此元素大的时候,则此元素向后移动,以空出多余的 ...

  4. 算法：冒泡排序（python版）

    1.将n个元素从大到小排序后,选择第k个大的元素 #!/usr/bin/env python #coding -*- utf:8 -*- #冒泡排序选第k个元素 import random impor ...

  5. Java基础知识强化61：经典查找之 常见查找算法小结

    一.顺序查找 条件:无序或有序队列. 原理:按顺序比较每个元素,直到找到关键字为止. 时间复杂度:O(n) 二.二分查找(折半查找) 条件:有序数组 原理:查找过程从数组的中间元素开始,如果中间元素正 ...

  6. 算法两数之和 python版

    方法一.暴力解法 -- 5s 复杂度分析:时间复杂度:O(n^2)空间复杂度:O(1) length = len(nums)for i in range(length):    for j in ra ...

  7. 常见排序算法（JS版）

    常见排序算法(JS版)包括: 内置排序,冒泡排序,选择排序,插入排序,希尔排序,快速排序(递归 & 堆栈),归并排序,堆排序,以及分析每种排序算法的执行时间. index.html <! ...

  8. 二分查找算法（Python版）

    [本文出自天外归云的博客园] 记性不好(@.@),所以平时根本用不到的东西就算学过如果让我去想也会需要很多时间(*.*)! 二分查找算法 在一个有序数组中查找元素最快的算法,也就是折半查找法,先找一个 ...

  9. 【数据结构与算法Python版学习笔记】查找与排序——散列、散列函数、区块链

    散列 Hasing 前言 如果数据项之间是按照大小排好序的话,就可以利用二分查找来降低算法复杂度. 现在我们进一步来构造一个新的数据结构, 能使得查找算法的复杂度降到O(1), 这种概念称为" ...

随机推荐

  1. 百度云BCC配置Apache VirtualHost 实现相同域名不同端口访问不同应用

    问题描述:前戏:本人在百度云上购买了BCC虚拟服务,并购买域名,部署应用,可以正常访问(这里一切都很正常^_^). 事情正在起变化:随着开发的不断推进,工程在本地测试成功后,部署到服务器,会发现有些页 ...

  2. [array] leetcode - 54. Spiral Matrix - Medium

    leetcode-54. Spiral Matrix - Medium descrition GGiven a matrix of m x n elements (m rows, n columns) ...

  3. 关于spring mybateis 定义resultType="java.util.HashMap"

    关于spring mybateis  定义resultType="java.util.HashMap" List<HashMap<String, Object>& ...

  4. 掌握numpy(二)

    目录 掌握numpy(一) 掌握numpy(二) 掌握numpy(三) 掌握numpy(四) 数组的reshape 顾名思义,就是对数组的形状进行改变,比如行变成列,一行变多行等. in place ...

  5. ArcGIS 网络分析[8.1] 资料1 使用AO打开或创建网络数据集之【打开】

    为了创建或打开一个网络数据集,你必须使用NetworkDatasetFDExtension对象(文件地理数据库中的数据集)或NetworkDatasetWorkspaceExtension对象(对于S ...

  6. java 类的继承和接口的继承

    父类 public class person { String name; int age; void eat(){ System.out.println("吃饭"); } voi ...

  7. python3.5 + PyQt5 +Eric6 实现的一个计算器

    目前可以实现简单的计算.计算前请重置,设计的时候默认数字是0,学了半天就做出来个这么个结果,bug不少. python3.5 + PyQt5 +Eric6 在windows7 32位系统可以完美运行 ...

  8. CentOS7源码安装lamp

    环境介绍 虚拟机 : VMware Workstation 14 Pro 镜像 : CentOS Linux release 7.4.1708 (Core) 物理机 : windows 7 64位 防 ...

  9. [js高手之路]原型式继承与寄生式继承

    一.原型式继承本质其实就是个浅拷贝,以一个对象为模板复制出新的对象 function object( o ){ var G = function(){}; G.prototype = o; retur ...

  10. spring中使用Hibernate中的getCurrentSession报出：createQuery is not valid without active transaction

    1.错误信息 HTTP Status 500 - createQuery is not valid without active transaction type Exception report m ...