Codeforces Round #431 (Div. 1)

A. From Y to Y

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

From beginning till end, this message has been waiting to be conveyed.

For a given unordered multiset of n lowercase English letters ("multi" means that a letter may appear more than once), we treat all letters as strings of length 1, and repeat the following operation n - 1 times:

• Remove any two elements s and t from the set, and add their concatenation s + t to the set.

The cost of such operation is defined to be 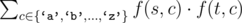, where f(s, c) denotes the number of times character cappears in string s.

Given a non-negative integer k, construct any valid non-empty set of no more than 100 000 letters, such that the minimum accumulative cost of the whole process is exactly k. It can be shown that a solution always exists.

Input

The first and only line of input contains a non-negative integer k (0 ≤ k ≤ 100 000) — the required minimum cost.

Output

Output a non-empty string of no more than 100 000 lowercase English letters — any multiset satisfying the requirements, concatenated to be a string.

Note that the printed string doesn't need to be the final concatenated string. It only needs to represent an unordered multiset of letters.

Examples

input

12

output

abababab

input

3

output

codeforces

Note

For the multiset {'a', 'b', 'a', 'b', 'a', 'b', 'a', 'b'}, one of the ways to complete the process is as follows:

• {"ab", "a", "b", "a", "b", "a", "b"}, with a cost of 0;
• {"aba", "b", "a", "b", "a", "b"}, with a cost of 1;
• {"abab", "a", "b", "a", "b"}, with a cost of 1;
• {"abab", "ab", "a", "b"}, with a cost of 0;
• {"abab", "aba", "b"}, with a cost of 1;
• {"abab", "abab"}, with a cost of 1;
• {"abababab"}, with a cost of 8.

The total cost is 12, and it can be proved to be the minimum cost of the process.

/*
* @Author: LyuC
* @Date:   2017-09-03 15:10:19
* @Last Modified by:   LyuC
* @Last Modified time: 2017-09-03 16:56:48
*/
/*
 题意：初始的时候一个集合内有n个元素(a-z的字符)，你可以进行这样的操作，每次取出集合内的
    两个元素删除，然后将这两个元素连起来作为一个元素放到集合内，此次操作的代价：
        f(s,c)*f(t,c),f(s,c)函数定义为，a-z每个字符在s中出现的次数的加和，现在给你一个
    代价k，让你构造出满足要求的字符串
 
 思路：n个相同的字符，构造的代价是n*(n-1)/2,然后这样就可以凑出k
*/
#include <bits/stdc++.h>
 
using namespace std;
 
int n;
string s;
int pos;
int i;
 
inline void init(){
    s="";
    pos=;
}
 
int main(){
    // freopen("in.txt","r",stdin);
    init();
    scanf("%d",&n);
    if(n==){
        puts("a");
        return ;
    }
    while(n>){
        i=;
        while(++i){
            if(i*(i-)/>n){
                break;
            }
        }
        i--;
        n-=i*(i-)/;
        while(i--){
            s+=pos%+'a';
        }
        pos++;
    }
    cout<<s<<endl;
    return ;
}