[Machine Learning]学习笔记-Neural Networks

引子

对于一个特征数比较大的非线性分类问题，如果采用先前的回归算法，需要很多相关量和高阶量作为输入，算法的时间复杂度就会很大，还有可能会产生过拟合问题，如下图：

这时就可以选择采用神经网络算法。
神经网络算法最早是人们希望模仿大脑的学习功能而想出来的。

一个神经元，有多个树突(Dendrite)作为信息的输入通道，也有多个轴突（Axon）作为信息的输出通道。一个神经元的输出可以作为另一个神经元的输入。神经元的概念和多分类问题的分类器概念很相近，都是可以接收多个输入，在不同的权值(weights)下产生出多个不同的输出。

模型表示

模型可以写成如下形式:
\[
\begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline \end{bmatrix}\rightarrow\begin{bmatrix}\ \ \ \newline \end{bmatrix}\rightarrow h_\theta(x)
\]
上图可以称为单隐层前馈网络，由输入层\(X\),输出层和它们之间的隐含层构成。

每个输出层都有一个权重矩阵(weights matrix)和一个偏置单元(bias unit)，用来计算输出。

前向传播

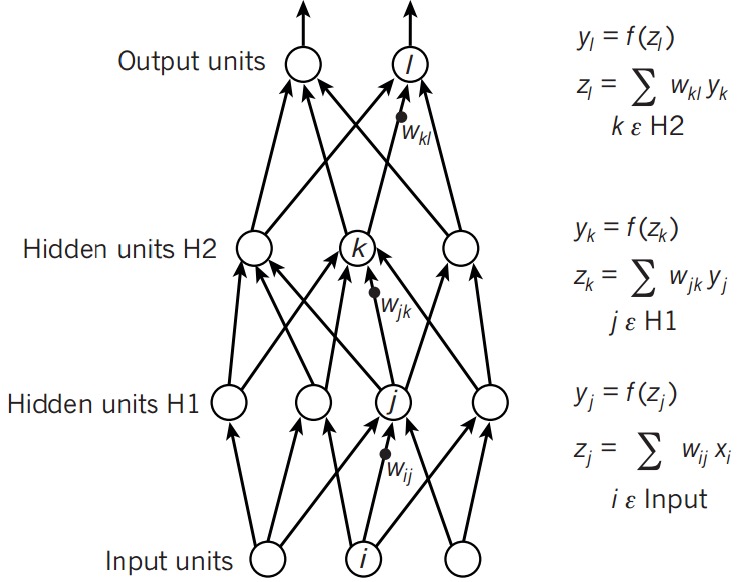
首先回顾一下Logistic Regression的单分类问题中\(h_\theta\)的计算：
\[\begin{align*}\begin{bmatrix}x_0 \newline x_1 \newline x_2\end{bmatrix} \rightarrow\begin{bmatrix}g(z^{(2)})\end{bmatrix} \rightarrow h_\Theta(x)\end{align*}\]

可以写为：
\[z^{(2)}=\omega^{(2)}a^{(1)}+b^{(2)}\\\
a^{(2)}=g(z^{(2)})\\\
h_\theta(x)=a^{(2)}
\]
而神经网络的前向传播，也就是在此基础上增加了层数，让一层的输出作为下一层的输入：
\[z^{(i)}=\omega^{(i)}a^{(i-1)}+b^{(i)}\\\
a^{(i)}=g(z^{(i)})\\\
z^{(i+1)}=\omega^{(i+1)}a^{(i)}+b^{(i+1)}\\\
...
\]
需要注意的是，每一层有多个单元，所以这里面的权重也是个二维矩阵。

反向传播（Backpropagation）

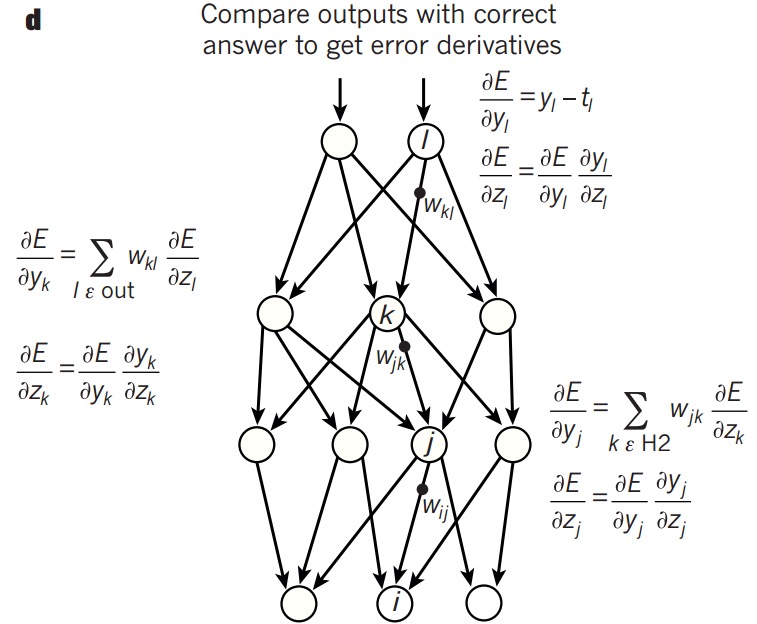
直观理解

但给予初始的偏置单元和权重矩阵后，预测值会不太理想。
那么，如何使预测值符合真实值呢？
\[z^{(i)}=\omega^{(i-1)}a^{(i-1)}+b^{(i-1)}\]
可以发现，可以通过改变每一层的\(a,\omega,b\)来改变最终的输出，但实际上\(a\)是不能直接改变的。
所以本质上要做的就是改变\(\omega\)和\(b\)来使预测值接近真实值。
思路和之前的logistic regression和线性回归模型一样，也是先构建代价函数，然后通过梯度下降法使代价方程的值降到最低点，也就得到了合适的\(\omega\)和\(b\)。
而使用梯度下降法时，需要计算每个\(\omega\)和\(b\)的梯度，梯度的绝对值越大，说明当前的代价函数对该参数的改变越敏感，改变这个参数使代价函数下降的越快。

微积分公式推导

以3B1B视频中的网络为例：

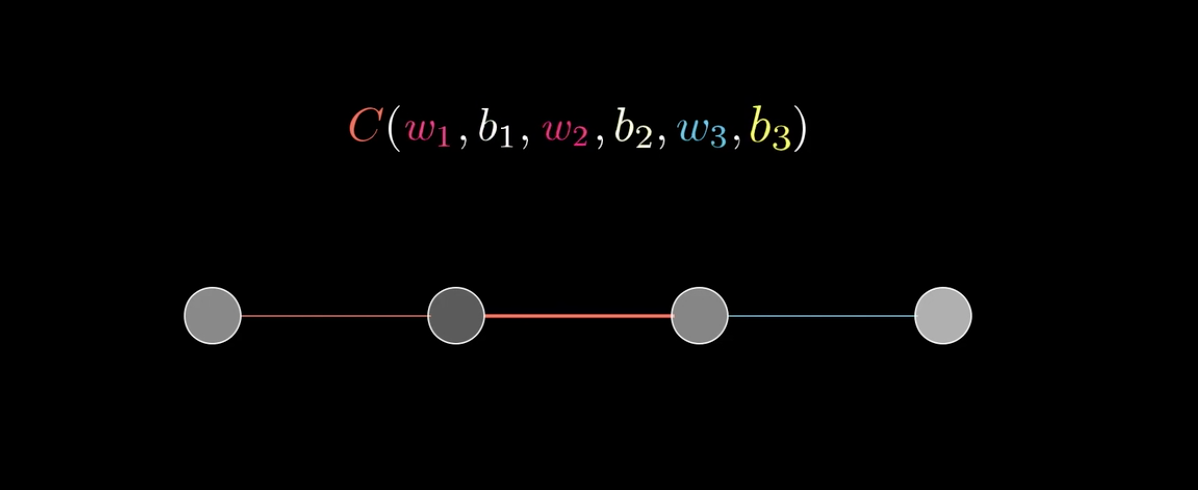
代价方程可以由最后一层的激活值\(a^{(L)}\)和真实值y的均方误差:\((a^{(L)}-y)^2\)表示。（PS：这里L=4,有些教材计算均方误差时乘上\(1/2\)）
然后，我们要求解\(\omega\)和\(b\)的梯度。
在这里以\(\frac{C_0}{\partial \omega^{(L)}}\)为例:

求梯度，也就是求代价函数对参数变化的敏感度。
可以发现，改变\(\omega^{(L)}\)，会先影响到\(z^{(L)}\),然后再影响到\(a^{(L)}\),最后影响\(C_0\)。
利用这个特性，可以将\(\frac{C_0}{\partial \omega^{(L)}}\)分解：

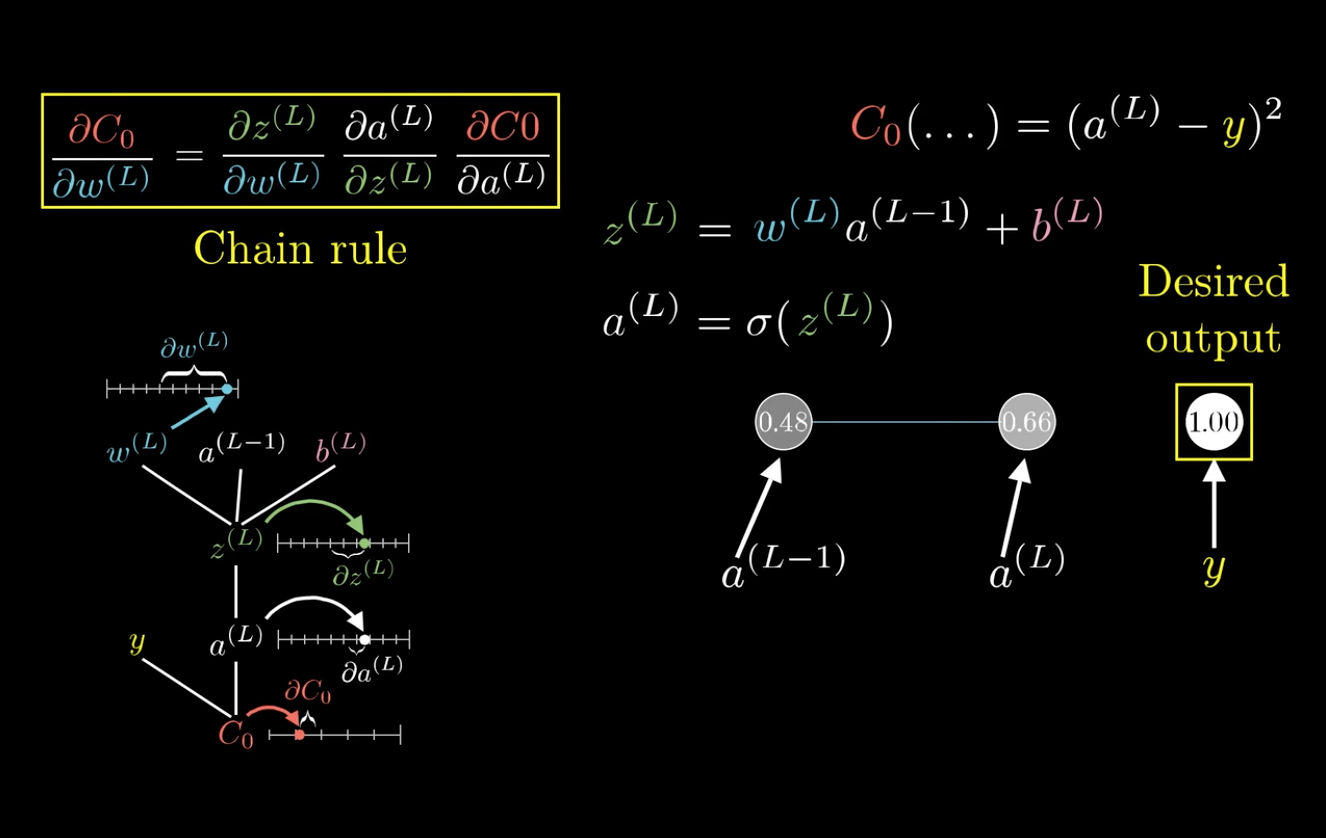
这就是所谓的链式法则(Chain rule):
\[\begin{split}
\frac{C_0}{\partial \omega^{(L)}}=&\frac{\partial z^{(L)}}{\partial \omega^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial C_0}{\partial a^{(L)}}\\\
=&a^{L-1}\sigma\prime(z^{(L)})2(a^{(L)}-y)
\end{split}\]

同样也可以求得\(b^{(L)}\)的梯度：

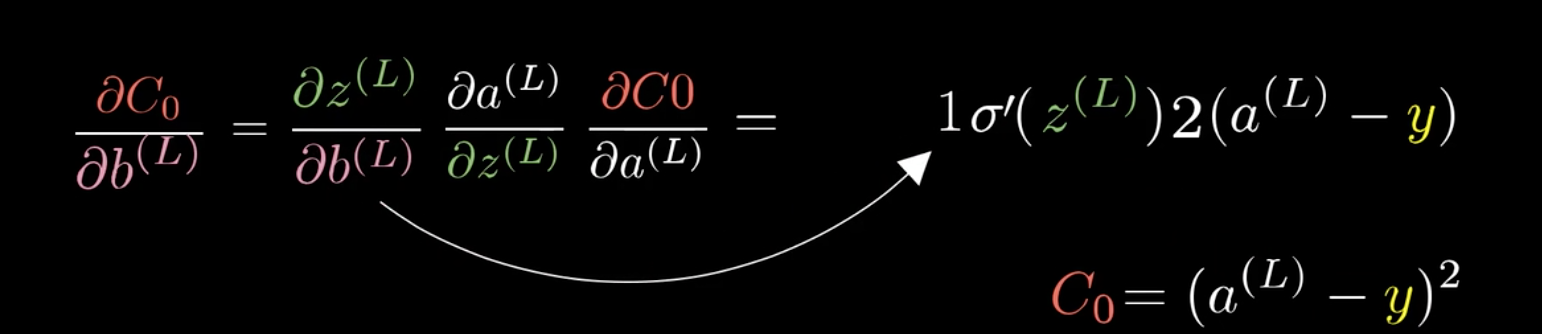
以上的网络每层只有一个神经元，如果有多个单元的话，以上的公式也是成立的。
之前提过，权重矩阵是二维的，可以给两个下标\(j,k\)表示\(\omega\):

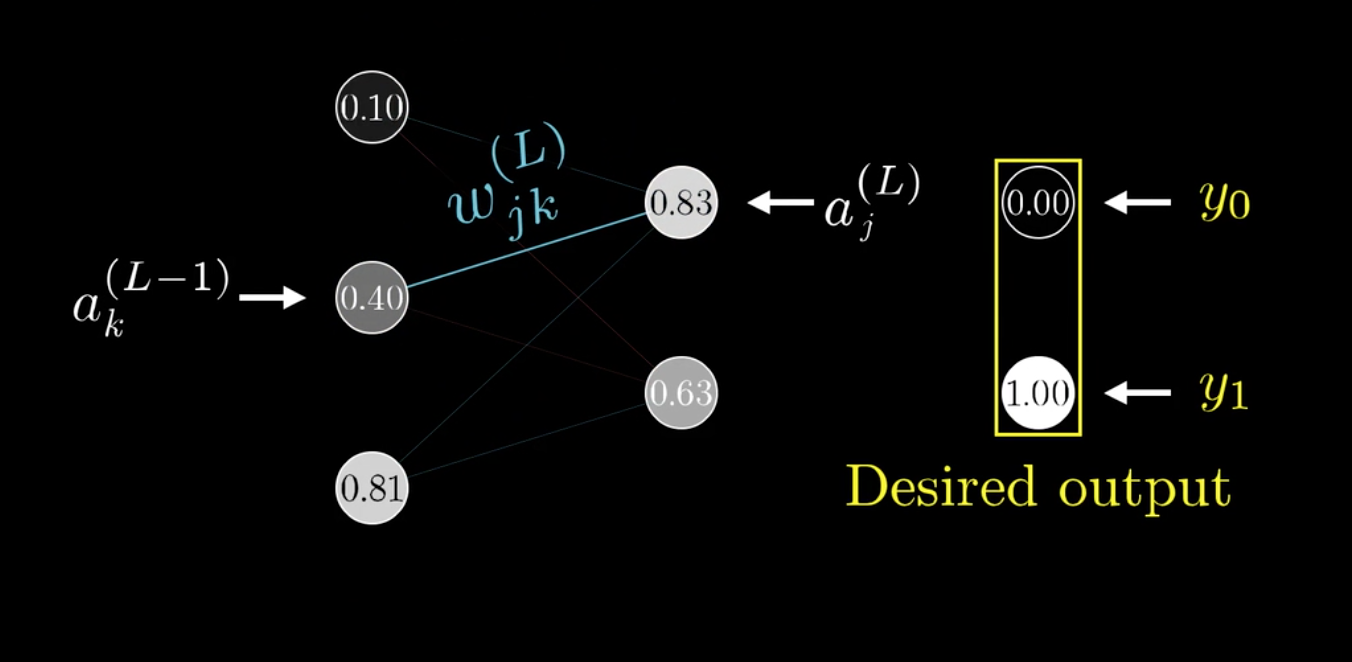
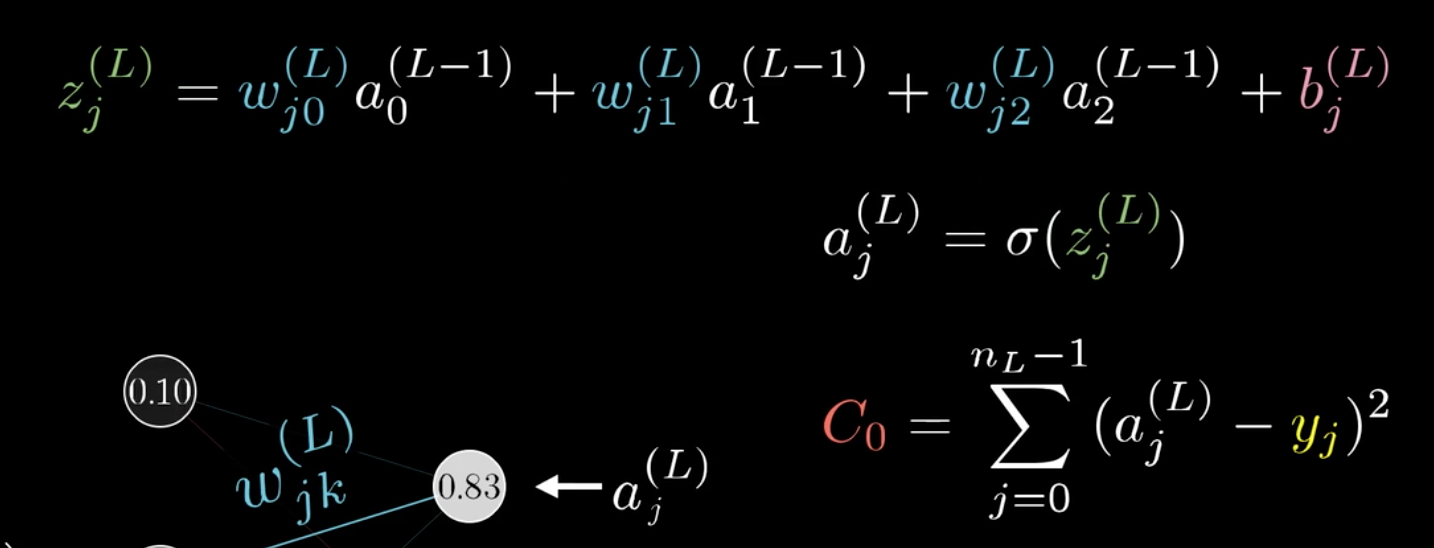
链式法则更新如下：
\[
\begin{split}\frac{C_0}{\partial \omega_{jk}^{(L)}}&= \frac{\partial z_j^{(L)}}{\partial \omega_{jk}^{(L)}}\frac{\partial a_j^{(L)}}{\partial z_j^{(L)}}\frac{\partial C_0}{\partial a_j^{(L)}}\\
&=a^{L-1}_k \sigma\prime(z^{(L)}_j)2(a^{(L)}_j-y_j)
\end{split}\]
而要把这个公式递推到其它层求\(\frac{C}{\partial \omega_{jk}^{(l)}}\)时，只需要变动公式中的\(\frac{\partial C}{\partial a_j^{(l)}}\)即可。
总结如下：

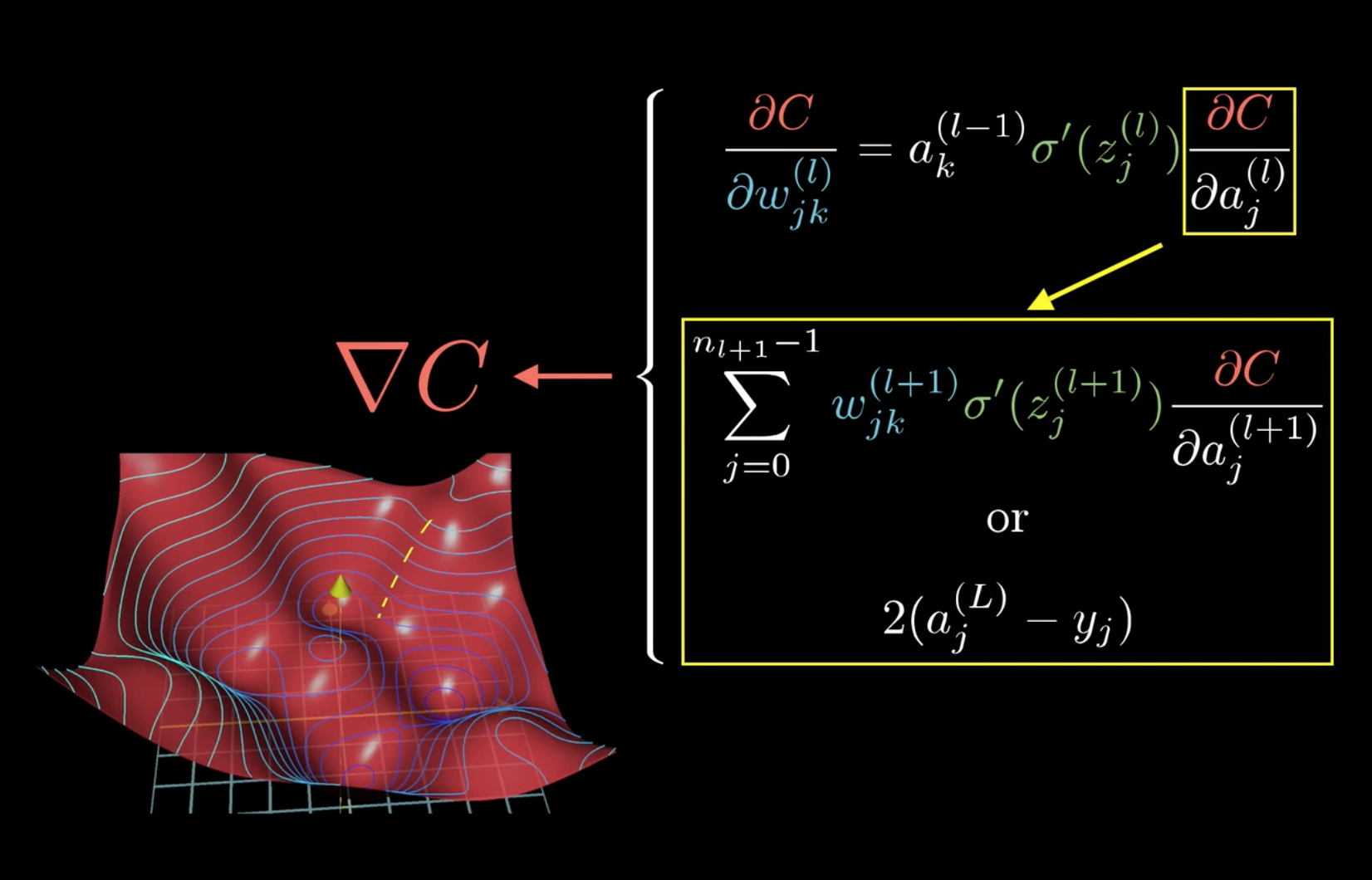
所以，可以发现，计算梯度时，前两项\(a^{l-1}_k ,\sigma\prime(z^{(l)}_j)\)是可以直接算出的，而最后一项，则可以先计算出\(\frac{\partial C0}{\partial a_j^{(L)}}\)，然后一层层向前传播即可，反向传播大概也就是这么个意思吧。
Andrew机器学习课程中给出了计算方法，也可以按这个思路去理解了。

TIPS:随机梯度下降法（Stochastic gradient descent）

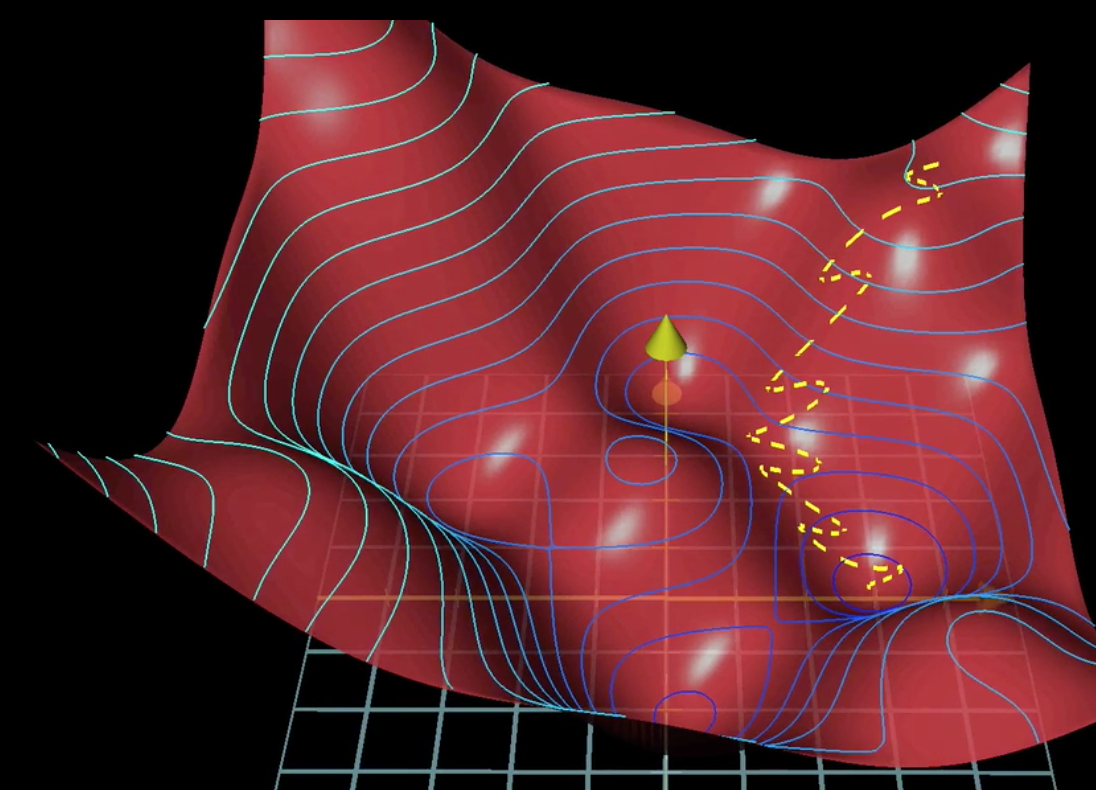
在之前的batch model中，每次更新权值都要遍历所有的样本然后取均值，这样效率太低，可以把样本分成数个大小相等的mini-batch，每次遍历完一个mini-batch，就更新下权值，虽然下降的路线未必最短，但速度上提升不少，这就是随机梯度下降算法。