题解 [SHOI2012]随机树

题目传送门

Description

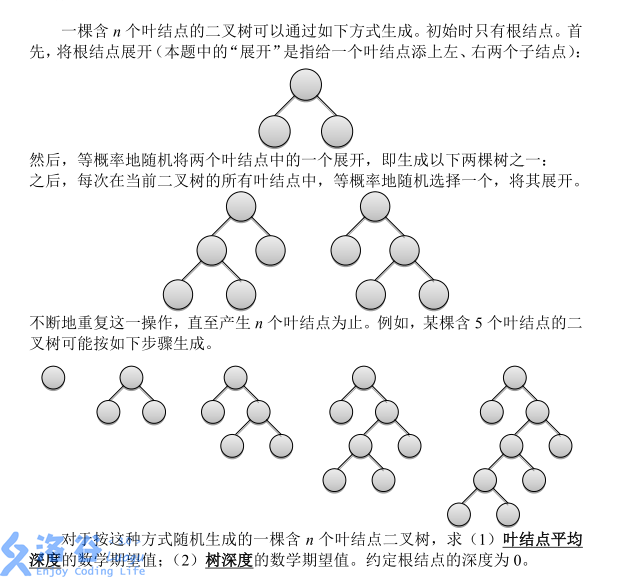
\(n\le 100\)

Solution

Problem 1

不难看出，答案就是：

\[1+\sum_{i=1}^{n-1} 2/(i+1)
\]

Problem 2

这个问真的很仙。

可（bu）以（neng） 想到，我们可以设 \(f_{i,j}\) 表示有 \(i\) 个叶子时深度 \(\ge j\) 的概率，可以得到转移式：

\[f_{i,j}=\frac{1}{i-1}\sum_{k=1}^{i-1} (f_{k,j-1}+f_{i-k,j-1}-f_{k,j-1}\times f_{i-k,j-1})
\]

可以直接除以 \(i-1\) 是因为可以证明把两颗子树合并，只要总大小相同，那么方案就相同。这里就不赘述了。

然后我们就可以得到答案就是：

\[\sum_{i=1}^{n-1} (f_{n,i}-f_{n,i+1})\times i
\]

Code

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define MAXN 105

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> inline void read (T &t,Args&... args){read (t);read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

double f[MAXN][MAXN];

signed main(){
	int q,up;read (q,up);
	if (q == 1){
		double d = 1;
		for (Int n = 2;n < up;++ n) d += 2.0 / (n + 1);
		printf ("%.6f\n",d);
	}
	else{
		for (Int i = 1;i <= up;++ i) f[i][0] = 1;
		for (Int i = 2;i <= up;++ i)
			for (Int j = 1;j < i;++ j){
				for (Int k = 1;k < i;++ k) f[i][j] += f[k][j - 1] + f[i - k][j - 1] - f[k][j - 1] * f[i - k][j - 1];
				 f[i][j] /= (i - 1);
			}
		double d = 0;
		for (Int i = 1;i < up;++ i) d += (f[up][i] - f[up][i + 1]) * i;
		printf ("%.6f\n",d);
	}
 	return 0;
}