Docker从入门到精通（七）—

什么是容器数据共享？简单来说就是容器与容器之间数据共享，容器与宿主机数据共享。

1、为什么需要数据共享？

①、数据持久化

比如我们有一个MySQL集群，通过容器启动，那么项目运行过程中的数据是保存在容器中的，假设容器被删除了，数据就丢失了，如果没有数据共享，那你就只能删库跑路了。

而有了数据共享，你就可以打通容器和宿主机的数据联通，将容器中的数据同步到宿主机，即使容器删除了，数据还是在本地的。

②、同步内容

前面的教程，我们每次要修改容器里面的内容，都得进入到容器中，而实际生产环境容器都是有很多个的，一个个修改，大家不用干活了。

那么你想不想在本地修改了，直接同步到容器？想就接着往下看。

2、命令挂载

docker run -it -v 宿主机目录:容器目录

比如我们将宿主机下面的 /home/webapps 目录挂载到Tomcat容器的 /usr/local/tomcat/webapps

docker run -it -v /home/webapps:/usr/local/tomcat/webapps -p 8083:8080 --name tomcat03 tomcat:latest /bin/bash

我们在容器的 /usr/local/tomcat/webapps 目录下新建 a.txt 文件，会在宿主机 /home/webapps 目录下找到这个文件；

同理在宿主机的 /home/webapps 目录下新建 b.txt 文件，你会在容器的 /usr/local/tomcat/webapps 目录下也能找到。

这样就完成了宿主机和容器文件目录的同步操作。

①、即使容器停止（不是删掉），宿主机挂载目录变动了，再次启动容器，宿主机改动还是能够同步到容器的。

②、容器删掉，宿主机挂载目录不会被删掉。

3、检查挂载是否成功

docker inspect 容器id

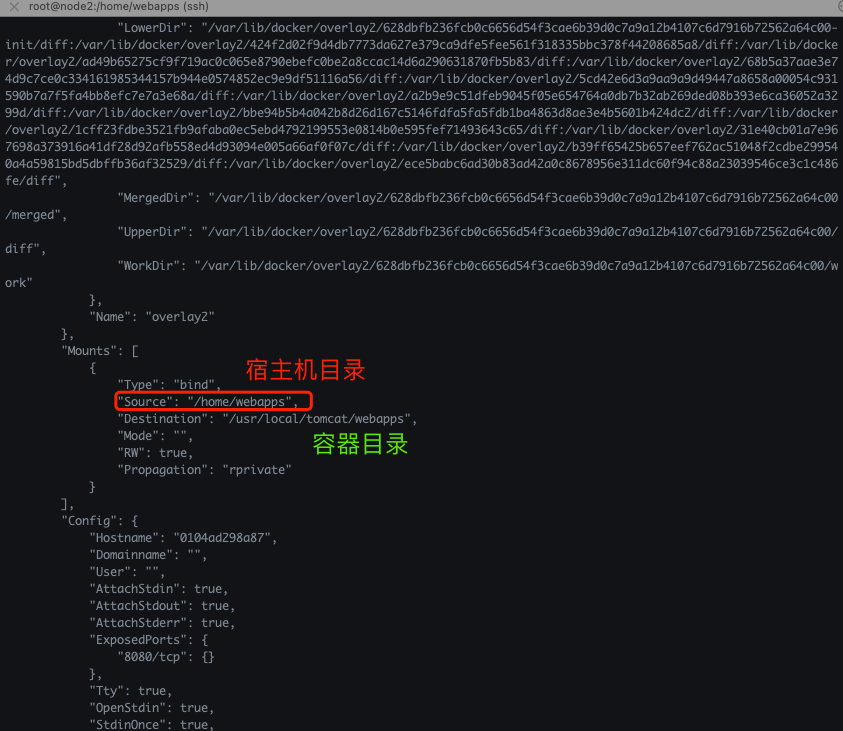
4、匿名挂载和具名挂载

4.1 匿名挂载

docker run -v 容器内路径

比如给一个Tomcat容器匿名挂载：

docker run -d -P -v /usr/local/tomcat/webapps tomcat:8.0

然后通过 docker inspect 容器id，查看挂载情况：

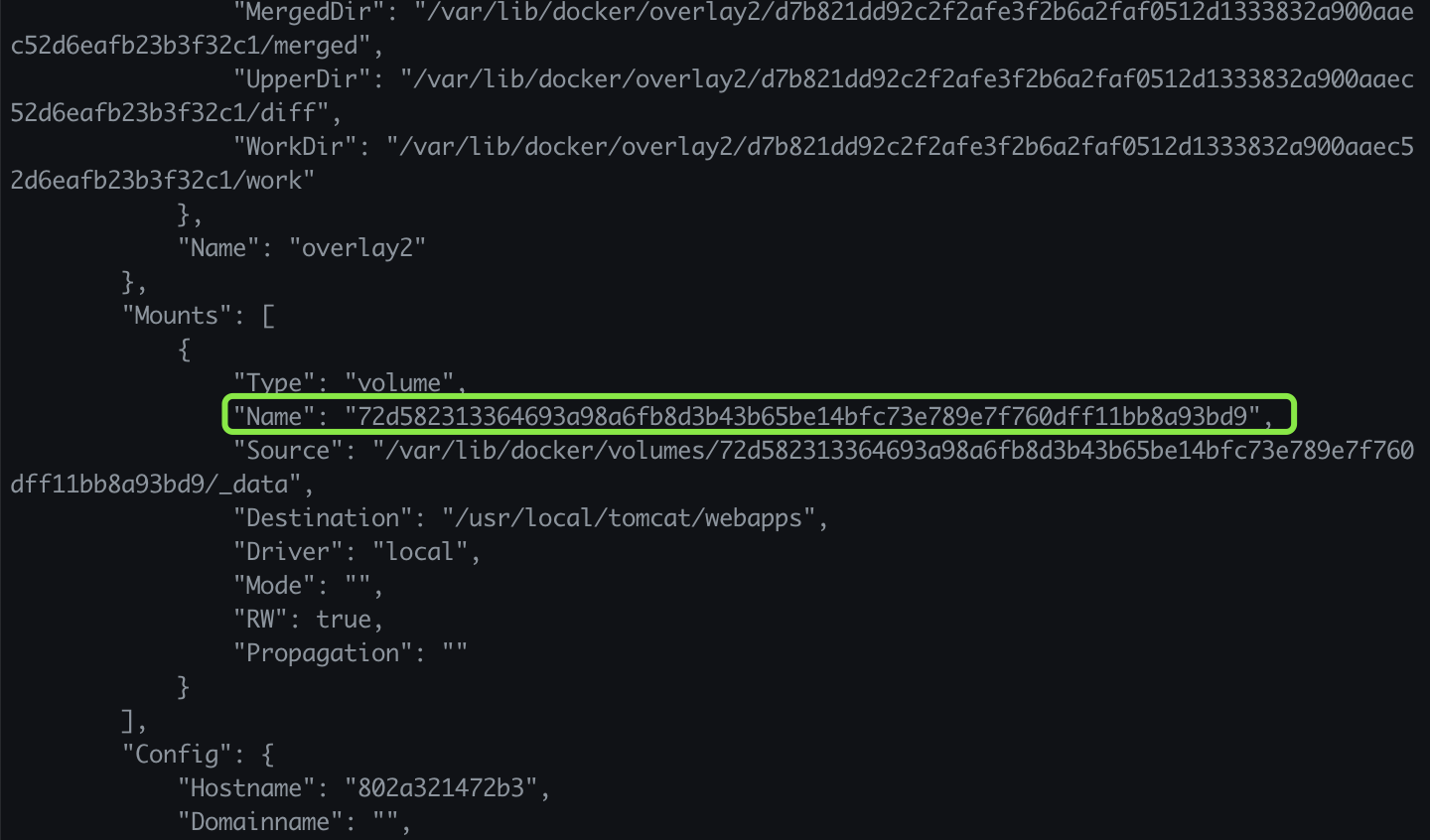
Name 属性为一长串数字的一般都是匿名挂载，可以到下面的Source属性指定的目录找到宿主机挂载目录。

4.2 具名挂载

docker run -v 卷名:容器内路径

指定Tomcat挂载名称为 tomcatVolumeUrl

docker run -d -P -v tomcatVolumeUrl:/usr/local/tomcat/webapps tomcat:8.0

同样通过 docker inspect 容器id查看：

5、共享容器进行挂载

大家有没有发现一个问题，通过上面的命令进行数据共享，如果我们有多个容器，都需要挂载一个目录，但是挂载过程中，有一个容器命令目录写错了，那就会造成容器数据不同步，如何解决这个问题呢？

答案就是创建一个共享容器，创建共享容器的同时进行目录挂载，然后别的容器和这个共享容器关联即可。

实例演示：

①、宿主机创建目录

我们在 /home 下创建 /share_volume 目录,然后在这个目录下新建 index.html 文件，里面就一句 hello docker!!!。

②、创建共享容器

docker create --name tomcat_share -v /home/share_volume:/usr/local/tomcat/webapps tomcat:latest /bin/true

③、创建实际容器

创建的同时指定和共享容器关联。

docker run -d -p 8081:8080 --volumes-from tomcat_share --name tomcat01 -d tomcat

docker run -d -p 8082:8080 --volumes-from tomcat_share --name tomcat02 -d tomcat

上面启动了两个容器，会发现更改宿主机的/home/share_volume 目录内容，两个容器的/usr/local/tomcat/webapps 目录内容都会改变。