AcWing03. 完全背包问题

有\(N\)种物品和一个容量是\(V\)的背包，每种物品都有无限件可用。

第\(i\)种物品的体积是\(v_i\)，价值是\(w_i\)。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行两个整数，\(N\)，\(V\)，用空格隔开，分别表示物品种数和背包容积。

接下来有\(N\)行，每行两个整数\(v_i\),\(w_i\)，用空格隔开，分别表示第\(i\)种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

\(0<N,V≤1000\)

\(0<v_i,w_i≤1000\)

输入样例

4 5

1 2

2 4

3 4

4 5

输出样例：

10

---

思路：



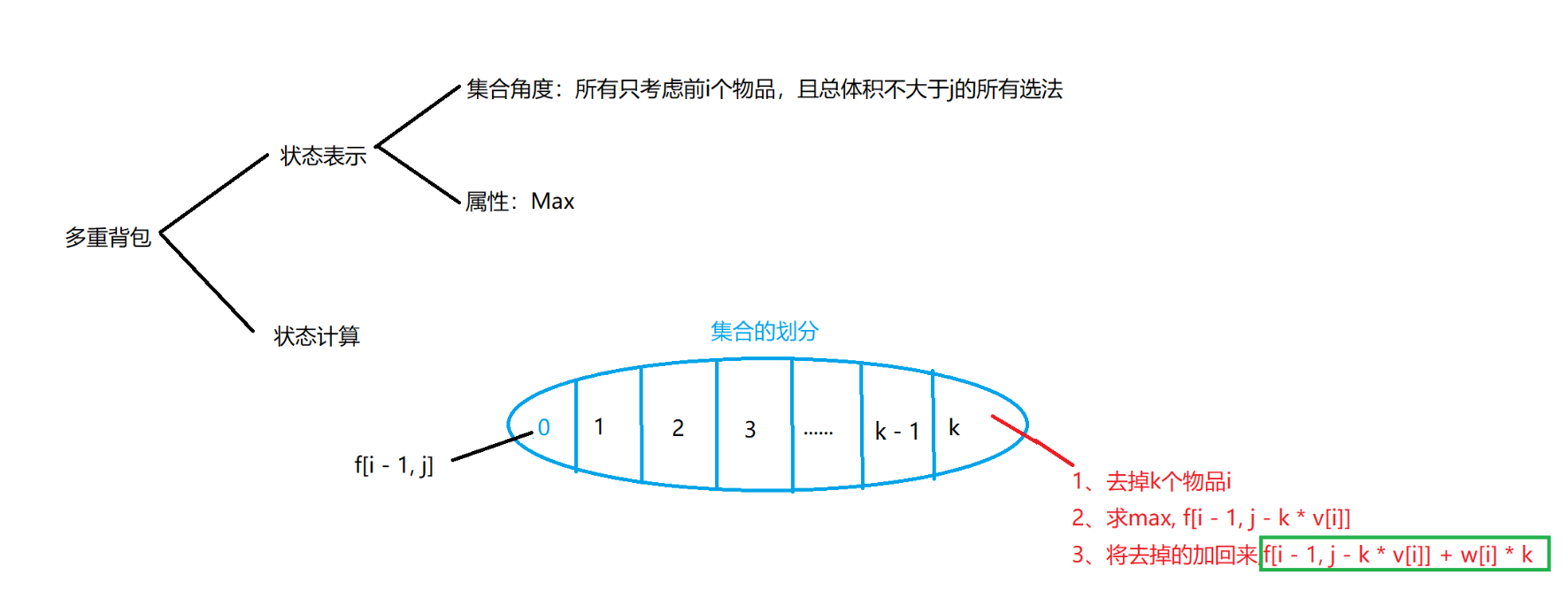
此时的\(0\)是不选第\(i\)件背包的情况(\(f[i - 1, j]\))、此时的\(k\)是不选第\(k\)件物品的情况、故可以列出状态转移方程为\(f[i - 1, j - k * v[i]] + k * w[i]\)。可以发现、时间复杂度过高、后面讨论优化的问题。

代码1：

#include<iostream>

using namespace std;

const int N = 1010;

int f[N][N];
int v[N],w[N];

int main()
{
    int n , m;
    cin>>n>>m;

    for(int i = 1 ; i <= n ;i ++) cin>>v[i]>>w[i];

    for(int i = 1 ; i <= n ;i++)
        for(int j = 0 ; j <= m ;j++)
            for(int k = 0 ; k*v[i] <= j ; k++)
                f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

    cout<<f[n][m]<<endl;
}

代码优化：



借助这层优化、我们舍去了k那层循环、大大的降低了时间复杂度(5倍的样子)，这样求得的最后的状态转移方程即为所求。

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N][N];

int main()
{
    int n, m;
    cin >> n >> m;

    for(int i = 1 ; i <= n ; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1 ; i <= n ; i ++ )
        for(int j = 0 ; j <= m ; j ++ )
        {
                f[i][j] = f[i - 1][j];
                if(j >= v[i])   // 物品体积得大于0
                {
                    f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
                }
        }
    cout << f[n][m] << endl;

    return 0;
}

与01背包的对比：