[刷题] 279 Perfect Squares

要求

• 给出一个正整数n，寻找最少的完全平方数，使他们的和为n

示例

• n = 12
• 12 = 4 + 4 + 4
• 输出：3

边界

• 是否可能无解

思路

• 贪心：12=9+1+1+1，无法得到最优解
• 图论：从n到0，每个数字表示一个节点，如果两个数字x到y相差一个完全平方数，则连接一条边
• 问题转化为无权图中从n到0的最短路径

  

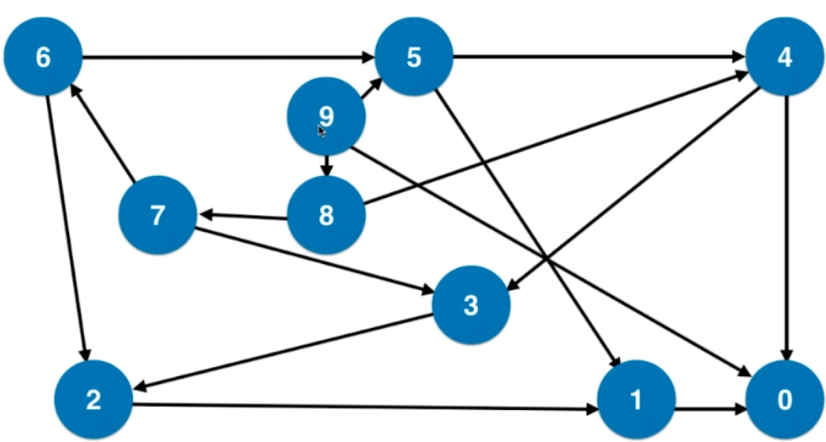
实现

• 队列中每个元素是一个pair对，保存具体数字和经历了几段路径走到这个数字

 1 class Solution {
 2 public:
 3     int numSquares(int n) {
 4
 5         assert( n > 0 );
 6
 7         queue< pair<int,int> > q;
 8         q.push( make_pair( n , 0 ) );
 9
10         while( !q.empty() ){
11             int num = q.front().first;
12             int step = q.front().second;
13             q.pop();
14
15             if( num == 0 )
16                 return step;
17
18             for( int i = 1 ; num - i*i >=0 ; i ++ )
19                 q.push( make_pair( num - i * i , step + 1 ) );
20         }
21
22         throw invalid_argument("No Solution");
23     }
24 };

• 有些节点被重复推入队列，n足够大时存在性能问题
• 不同于树，图中每个节点都有多种路径到达

优化

• 用一个辅助向量 visited 记录节点是否推入过队列
• 用变量记录num-i*i，减少计算
• 推入0时，直接返回结果，而不需要在循环处先取出

 1 class Solution {
 2 public:
 3     int numSquares(int n) {
 4
 5         assert( n > 0 );
 6
 7         queue< pair<int,int> > q;
 8         q.push( make_pair( n , 0 ) );
 9
10         vector<bool> visited(n+1, false);
11         visited[n] = true;
12
13         while( !q.empty() ){
14             int num = q.front().first;
15             int step = q.front().second;
16             q.pop();
17
18             for( int i = 1 ; ; i ++ ){
19                 int a = num - i*i;
20                 if( a < 0 )
21                     break;
22                 if( a == 0)
23                     return step + 1;
24                 if( ! visited[a] ){
25                 q.push( make_pair( a , step + 1 ) );
26                 visited[a] = true;
27             }
28         }
29     }
30     throw invalid_argument("No Solution");
31     }
32 };

相关

• 127 Word Ladder
• 126 Word Ladder II