NOIP模拟测试38「金·斯诺·赤」

金

辗转相减见祖宗

高精

#include<bits/stdc++.h>
using namespace std;
#define A 2000
#define P 1
#define N 10
#define ll long long
ll n,T;
char sjdfj[A];
struct bignum
{
    ll n[A],l;
    bignum(){l=1,memset(n,0,sizeof(n));}
    void clear(){while(l>1&&!n[l-1]) l--;}
    void print(){
        printf("%lld",n[l-1]);
        for(ll i=l-2;i>=0;i--){
            printf("%0*lld",P,n[i]);
        }
        printf("\n");
    }
    void read(){
        l=0;
        scanf("%s",sjdfj+1);
        l=strlen(sjdfj+1);
        reverse(sjdfj+1,sjdfj+l+1);
        for(ll i=0;i<l;i++){
            n[i]=sjdfj[i+1]-'0';
        }
    }
    ll ok(){
        //若为0 return1
        //若%2==0 return2
        //若%2!=0 return3
        if(n[0]==0&&l==1) return 1;
//        if(n[0]==1&&l==1) return 1;
        if(n[0]%2==0) return 2;
        if(n[0]%2!=0) return 3;
    }
    bool operator <(bignum x) const
    {
        bignum t=*this,tep;
        if(t.l!=x.l)    return t.l<x.l;
        for(ll i=t.l-1;i>=0;i--)
        {
            if(t.n[i]!=x.n[i]) return t.n[i]<x.n[i];
        }
        return 0;
    }
    bool operator >(bignum x) const
    {
        bignum t=*this;
        if(t.l!=x.l) return t.l>x.l;
        for(ll i=t.l-1;i>=0;i--)
        {
            if(t.n[i]!=x.n[i]) return t.n[i]>x.n[i];
        }
        return 0;
    }
    bignum operator -(bignum x) const
    {
        bignum t=*this;
        if(t<x) swap(t,x);
        ll jie=0;
    //    t.print();x.print();
        for(ll i=0;i<t.l;i++)
        {
            t.n[i]-=x.n[i];
            while(t.n[i]<0)
            {
                t.n[i]+=N;
                jie++;
            }
            t.n[i+1]-=jie;
            jie=0;

        }
        while(!t.n[t.l-1]&&t.l>1) t.l--;
        return t;
    }
    bignum operator *(bignum x) const{
        bignum t=*this,tep;
        tep.l=t.l+x.l+1;
        for(ll i=0;i<t.l;i++)
            for(ll j=0;j<x.l;i++){
                tep.n[i+j]+=t.n[i]*x.n[j];
            }
        for(ll i=0;i<tep.l;i++){
            if(tep.n[i]>=N)
            {
                tep.n[i+1]+=tep.n[i]/N;
                tep.n[i]%=N;
            }
        }
        tep.clear();
        return tep;
    }
    bignum operator +(bignum x)const{
        bignum t=*this;
        if(t.l<x.l) t.l=x.l;
        t.l++;
        for(ll i=0;i<t.l;i++){
            t.n[i]+=x.n[i];
            if(t.n[i]>=N){
                t.n[i+1]+=t.n[i]/N;
                t.n[i]%=N;
            }
        }
        t.clear();
        return t;
    }
    bignum operator =(ll x){
        l=0;
        while(x){
            n[l++]=x%N;
            x/=N;
        }
        return *this;
    }
    bignum operator *(const ll &b){
        bignum t=*this,r;
        r.l=0;
        ll g=0;
        for(ll i=0;i<t.l||g;i++){
            ll x;
            if(i<t.l)
                x=t.n[i]*b+g;
            else x=g;
            r.n[r.l++]=x%N;
            g=x/N;
        }
        return r;
    }
    bignum operator /(const ll &x){
        bignum t=*this,r;
        ll tmp=0;
        r.l=t.l;
        for(ll i=t.l-1;i>=0;i--){
            tmp+=t.n[i];
            if(tmp>=x){
                r.n[i]=tmp/x;
                tmp%=x;
            }
            tmp*=N;
        }
        r.clear();
        return r;
    }
}a,b,c;
ll gcd(){
        //若为0 return1
        //若%2==0 return2
        //若%2!=0 return3
    while((a.ok()!=1&&b.ok()!=1)){
//        printf("a=%lld ",a.ok());
//        a.print();
//        printf("b=%lld ",b.ok());
//        b.print();
        ll ok1=a.ok(),ok2=b.ok();
        if(ok1==2&&ok2==2){
            return 0;
            a=a/2,b=b/2;
        }
        else if(ok1==3&&ok2==3){
            if(a<b) swap(a,b);
            a=a-b;
        }
        else if(ok1==2&&ok2==3){
            a=a/2;
        }
        else if(ok1==3&&ok2==2){
            b=b/2;
        }
    }
}
int main()
{/*1 1023 3072*/
//    freopen("bf.txt","w",stdout);
    scanf("%lld",&T);
    for(ll i=1;i<=T;i++){
        a.read(),b.read();
    //    a=a-b;
        gcd();
//        a.print(),b.print();
        if(a.n[0]==0&&b.n[0]==1&&b.l==1&&a.l==1){
            printf("Yes\n");
        }
        else if(a.n[0]==1&&b.n[0]==0&&b.l==1&&a.l==1){
            printf("Yes\n");
        }
        else printf("No\n");
    }
}

斯诺

考试代码改了改,数组开小见祖宗

考试时候$re$了

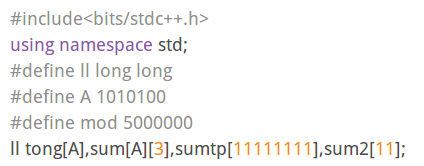
大概就是这样

考试时也维护的前缀和

$60\%$算法

只含$0,1$

我们可以将$0$看作减$1$,$1$看作加一

那么合法方案数就是$sum[r]-sum[l-1]==0$的个数

我们开一个桶存$sum[l]$,那么当前符合就是桶里$sum[i]$个数

查完个数再把$sum[r]$压进桶就行了

注意初始化,当你$sum==0$时也是合法方案,方案数为桶里$sum==0$个数$+1$,你可以先在桶里$0$压一个再进行操作

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 5000000
ll tong[mod+mod+mod+mod],sum[mod+mod][3],sumtp[21111111],sum2[111111111];
ll n,ans=0,all;
char a[mod+mod];
void solve(ll ql,ll qr){
    if(ql==qr) return ;
    ll mid=(ql+qr)>>1;
    solve(ql,mid);solve(mid+1,qr);
    ans=rand();
}
ll check(ll l,ll r){
    ll len=(r-l+1)/2;
//    printf("l=%lld r=%lld len=%lld\n",l,r,len);
//    printf("sum0=%lld 1=%lld 2=%lld\n",sum[r][0]-sum[l-1][0],sum[r][1]-sum[l-1][1],sum[r][2]-sum[l-1][2]);
    if(sum[r][0]-sum[l-1][0]>len) return 0;
    if(sum[r][1]-sum[l-1][1]>len) return 0;
    if(sum[r][2]-sum[l-1][2]>len) return 0;
    return 1;
}
int main(){
    scanf("%lld",&n);
    scanf("%s",a+1);
    all=1;
    for(ll i=1;i<=n;i++){
        sum[i][0]=sum[i-1][0];
        sum[i][1]=sum[i-1][1];
        sum[i][2]=sum[i-1][2];
        if(a[i]=='0') sum[i][0]++;
        if(a[i]=='1') sum[i][1]++;
        if(a[i]=='2') sum[i][2]++,all=0;
    }
    if(all&&n>1000){
        tong[mod]=1;
        for(ll i=1;i<=n;i++){
            sumtp[i]=sumtp[i-1];
            if(a[i]=='0') {
//                if(a[i-1]=='1') sumtp[i]=0;
//                if(sumtp[i]<0) ans++;
                sumtp[i]++;
            }
            else {
//                if(a[i-1]=='0') sumtp[i]=0;
//                if(sumtp[i]>0) ans++;
                sumtp[i]--;
            }
        }
        for(ll i=1;i<=n;i++){
            ans+=tong[mod+sumtp[i]];
            tong[mod+sumtp[i]]++;
//            printf("sumtp=%lld\n",sumtp[i]);

        }
        printf("%lld\n",ans);
        return 0;
    }
    if(n<=1000)
    for(ll i=1;i<=n;i++){
        for(ll j=i+1;j<=n;j++){
            if(check(i,j)){
                ans++;
            }
        }
    }
    else solve(1,n);
    printf("%lld\n",ans);
}

从$40\%$算法寻找思路

$60\%$算法$2$

维护三个$sum$,当为$0$,$sum[0]-- sum[1]++ sum[2]++$这样就又和上面类似了

然而合法方案数不止$sum[r]-sum[l-1]==0$

合法很难维护找非法的,最后答案就是合法减非法

发现非法$sum$相减肯定$<0$

那么就转化为逆序对问题

树状数组求逆序对

(其实你常数优秀可以$AC$

$100\%$算法

发现前后差异不大,假设你当前答案$1$为QAQ,若这一位仍为$1$,答案就要对应$-$,另外$2$,$0$答案就要$+$