1352 - Colored Cubes (枚举方法)

There are several colored cubes. All of them are of the same size but they may be colored differently. Each face of these cubes has a single color. Colors of distinct faces of a cube may or may not be the same.

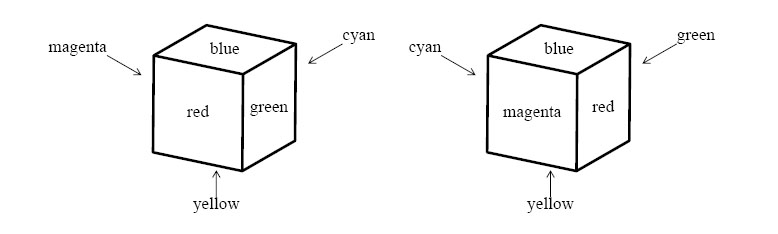
Two cubes are said to be identically colored if some suitable rotations of one of the cubes give identical looks to both of the cubes. For example, two cubes shown in Figure 2 are identically colored. A set of cubes is said to be identically colored if every pair of them are identically colored.

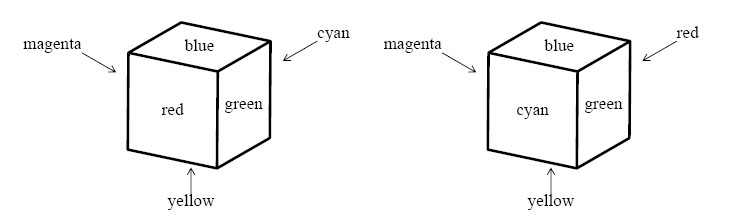
A cube and its mirror image are not necessarily identically colored. For example, two cubes shown in Figure 3 are not identically colored.

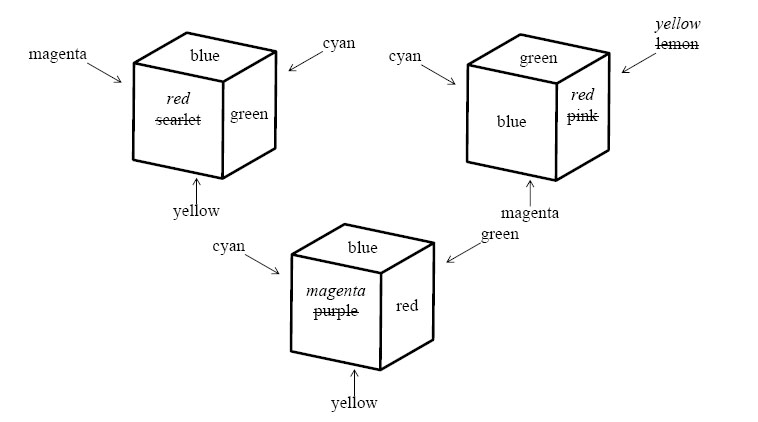
You can make a given set of cubes identically colored by repainting some of the faces, whatever colors the faces may have. In Figure 4, repainting four faces makes the three cubes identically colored and repainting fewer faces will never do.

Your task is to write a program to calculate the minimum number of faces that needs to be repainted for a given set of cubes to become identically colored.

Input

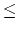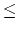The input is a sequence of datasets. A dataset consists of a header and a body appearing in this order. A header is a line containing one positive integer n and the body following it consists of n lines. You can assume that 1n4 . Each line in a body contains six color names separated by a space. A color name consists of a word or words connected with a hyphen (-). A word consists of one or more lowercase letters. You can assume that a color name is at most 24-characters long including hyphens.

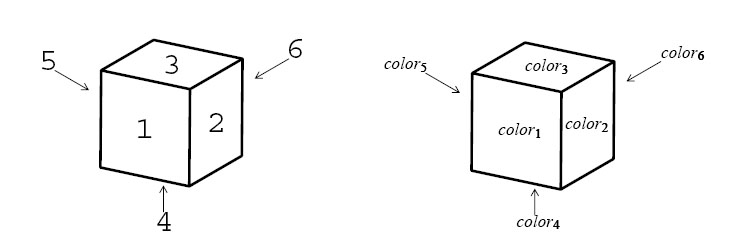
A dataset corresponds to a set of colored cubes. The integer n corresponds to the number of cubes. Each line of the body corresponds to a cube and describes the colors of its faces. Color names in a line is ordered in accordance with the numbering of faces shown in Figure 5. A line

color₁ color₂ color₃ color₄ color₅ color₆

corresponds to a cube colored as shown in Figure 6.

The end of the input is indicated by a line containing a single zero. It is not a dataset nor a part of a dataset.

Figure 2: Identically colored cubes

Figure 3: cubes that are not identically colored

Figure 4: An example of recoloring

Figure 5: Numbering of faces Figure 6: Coloring

Output

For each dataset, output a line containing the minimum number of faces that need to be repainted to make the set of cub es identically colored.

Sample Input

3
scarlet green blue yellow magenta cyan
blue pink green magenta cyan lemon
purple red blue yellow cyan green
2
red green blue yellow magenta cyan
cyan green blue yellow magenta red
2
red green gray gray magenta cyan
cyan green gray gray magenta red
2
red green blue yellow magenta cyan
magenta red blue yellow cyan green
3
red green blue yellow magenta cyan
cyan green blue yellow magenta red
magenta red blue yellow cyan green
3
blue green green green green blue
green blue blue green green green
green green green green green sea-green
3
red yellow red yellow red yellow
red red yellow yellow red yellow
red red red red red red
4
violet violet salmon salmon salmon salmon
violet salmon salmon salmon salmon violet
violet violet salmon salmon violet violet
violet violet violet violet salmon salmon
1
red green blue yellow magenta cyan
4
magenta pink red scarlet vermilion wine-red
aquamarine blue cyan indigo sky-blue turquoise-blue
blond cream chrome-yellow lemon olive yellow
chrome-green emerald-green green olive vilidian sky-blue
0

Sample Output

4
2
0
0
2
3
4
4
0
16

题意:给定几个彩色立方块，求最少涂色次数使得所有立方块一样。

思路：暴力枚举，n最大4.每个立方块最多有24种摆放方式，如第一个作为参照物不用旋转，所以复杂度为O(24^3)、然后枚举过程，先把旋转方式打出表来，之后就是暴力枚举了。

代码：

#include <stdio.h>
#include <string.h>
#include <string>
#include <map>
#define INF 0x3f3f3f3f
#define min(a,b) (a)<(b)?(a):(b)
#define max(a,b) (a)>(b)?(a):(b)
using namespace std;

const int left[6] = {1, 5, 2, 3, 0, 4};
const int up[6] = {3, 1, 0, 5, 4, 2};

map<string, int> vis;
map<string, int> color;
int dice24[24][6], block[4][6], ans;
int n, r[6];

void rot(const int *T, int *p) {
    int q[6];
    memcpy(q, p, sizeof(q));
    for (int i = 0; i < 6; i ++)
	p[i] = T[q[i]];
}

void dice_table() {
    int n = 0;
    int p0[6] = {0, 1, 2, 3, 4, 5};
    for (int i = 0; i < 6; i ++) {
	int p[6]; memcpy(p, p0, sizeof(p0));
	if (i == 0) rot(up, p);
	if (i == 1) {rot(left, p); rot(up, p);}
	if (i == 3) {rot(up, p); rot(up, p);}
	if (i == 4) {rot(left, p); rot(left, p); rot(up, p);}
	if (i == 5) {rot(left, p); rot(left, p); rot(left, p); rot(up, p);}
	for (int j = 0; j < 4; j ++) {
	    for (int k = 0; k < 6; k ++)
		dice24[n][k] = p[k];
	    rot(left, p);
	    n ++;
	}
    }
}

void init() {
    vis.clear();
    color.clear();
    ans = INF;
    int colorn = 0; char str[105];
    for (int i = 0; i < n; i ++)
	for (int j = 0; j < 6; j ++) {
	    scanf("%s", str);
	    if (!vis[str]) {
		block[i][j] = colorn;
		color[str] = colorn ++;
		vis[str] = 1;
	    }
	    else block[i][j] = color[str];
	}
}

void check() {
    int p[4][6], count = 0;
    memset(p, 0, sizeof(p));
    for (int i = 0; i < 6; i ++)
	p[0][i] = block[0][i];
    for (int i = 1; i < n; i ++) {
	for (int j = 0; j < 6; j ++)
	    p[i][dice24[r[i]][j]] = block[i][j];
    }
    int color[24];
    for (int i = 0; i < 6; i ++) {
	memset(color, 0, sizeof(color));
	for (int j = 0; j < n; j ++)
	    color[p[j][i]] ++;
	int Max = 0;
	for (int j = 0; j < 24; j ++) {
	    Max = max(Max, color[j]);
	}
	count += (n - Max);
    }
    ans = min(count, ans);
}

void dfs(int i) {
    if (i == n) {check(); return;}
    for (int j = 0; j < 24; j ++) {
	r[i] = j;
	dfs(i + 1);
    }
}

void solve() {
    dfs(1);
    printf("%d\n", ans);
}
int main() {
    dice_table();
    while (~scanf("%d", &n) && n) {
	init();
	solve();
    }
    return 0;
}