选择类排序 （简单选择排序，堆排序）— c语言实现

选择类排序包括：

(1)  简单选择排序

（2）树形选择排序

（3）堆排序

简单选择排序：

【算法思想】：在第 i 趟简单选择排序中，从第 i 个记录开始，通过 n - i 次关键字比较，从 n - i + 1 个记录中选出关键字最小的记录，并和第 i 个记录进行交换

时间复杂度：O(n^2)

 //此函数中a[0]不用，即对 a[1] ~ a[length-1] 排序；
   //如果对a[0]~a[length-1]排序，将 for 循环中的 i = 1 改为 i = 0 即可，注意输出
 void select(int a[],int length){//length为数组的长度
     int i,j;
     int min;//记录最小值的位置

     for(i = ;i < length - ;i++){
         min = i;
         //选择最小的值
         for(j = i + ;j < length;j++){
             if(a[j] < a[min]) //更新最小值的坐标
                 min = j;
         }
         if(min != i){
             int temp;
             temp = a[min];
             a[min] = a[i];
             a[i] = temp;
         }
     }
 }

堆排序:

堆排序是威洛母斯在1964年提出的对树形选择排序的改进算法，其只需要一个记录大小的辅助空间，采用向量数组方式存储，采用完全二叉树的顺序结构的特征进行分析，而非采用树的存储结构。

从小到大排序采用大根（顶）堆：r[i].key >= r[2i].key && r[i].key >= r[2i+1].key (结点值大于等于其左子与右子）

从大到小排序采用小根（顶）堆：r[i].key <= r[2i].key && r[i].key<= r[2i+1].key (结点值小于等于其左子与右子）

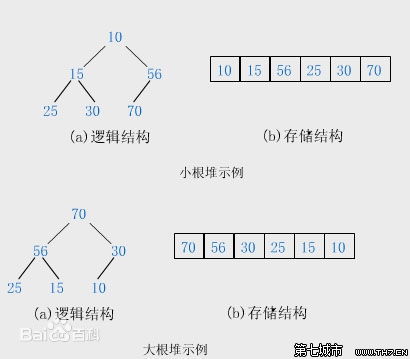
【算法思想】把待排序的记录的关键字存放在数组 r[1...n] 中，将 r 看成一棵完全二叉树的顺序表示，每个结点表示一个记录，第一个记录 r[1] 作为二叉树的根，以下各记录 r[2] ~ r[n] 依次逐层从左到右顺序排列，任意结点 r[i] 的左孩子是 r[2i] ,右孩子是 r[2i+1]，双亲是 r[i/2]。对这棵二叉树进行调整建堆。

时间复杂度：O（nlog₂n)

　　说明：在c语言中，i/2 的含义是整除，不同于数学中的定义，即 3/2 = 1，有一个向下取整的意思

堆排序可分为2步（从小到大排序）：

<1> 建初堆：建立一个大根堆

<2>重建堆：进行 n - 1 趟的交换（r[1] 与 堆尾进行交换）和建堆的过程

 /*堆排序*/
 /*建初堆：大根堆*/
 void AdjustDown(int a[],int k,int len);
 void BuildMaxHeap(int a[],int len){
     int i;
     for(i = len/;i > ;i--){
         AdjustDown(a,i,len);
     }
 }
 //调整堆
 void AdjustDown(int a[],int k,int len){
     a[] = a[k];//将第一个记录移出
     int i;
     for(i = *k;i <= len;i = *i){
         if(i < len && a[i] < a[i+])//不能忘记i < len,否则会超出范围
             i++;//取左右子中的最大值
         if(a[] >= a[i])
             break;
         else{
             a[k] = a[i]; //将a[i]调整到其双亲结点上
             k = i; //修改k值，以便继续向下筛选
         }
     }
     a[k] = a[];
 }

 void HeapSort(int a[],int len){
     BuildMaxHeap(a,len);
     int i;
     int temp;
     for(i = len;i > ;i--){
         //第一个和堆尾进行交换
         temp = a[];
         a[] = a[i];
         a[i] = temp;
         //调整堆
         AdjustDown(a,,i-);
     }
 }

图可参照：https://blog.csdn.net/u013384984/article/details/79496052

测试：

 int main(){
     int a[] = {-,,,,,,,,,,};
     int b[] = {-,,,,,,,,,,};
     int i,j;
     select(a,); //没有用a[0],对后面的元素进行排序
     HeapSort(b,);//数组的最后一个下标，a[0]为辅助单元
     for ( i = ;i < ;i++){
         printf("%d \t",a[i]);
     }
     printf("\n");

     for ( i = ;i < ;i++){
         printf("%d \t",b[i]);
     }
     printf("\n");
 }