2019 SDN上机第一次实验作业

1. 安装轻量级网络仿真工具Mininet

先从GitHub上获取mininet源码，再输入命令进行安装，代码分别如下：

git clone https://github.com/mininet/mininet.git

cd mininet/util
./install.sh

运行结果如下：

2. 用字符命令搭建如下拓扑，要求写出命令

（1）拓扑结构如下：

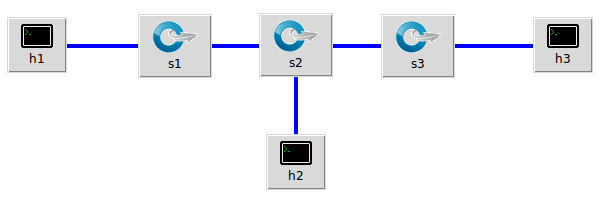
输入命令：

sudo mn --topo linear,3

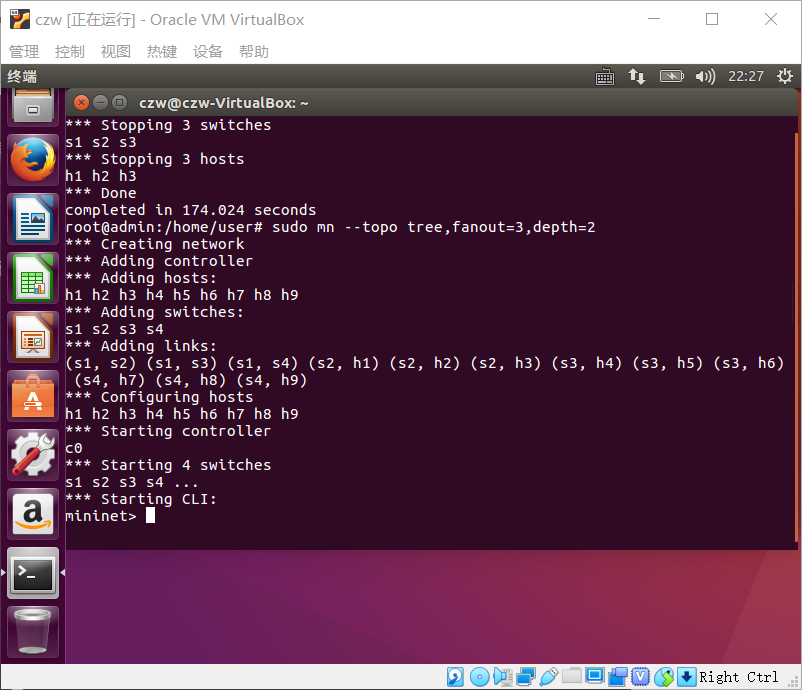
（2）拓扑结构如下：

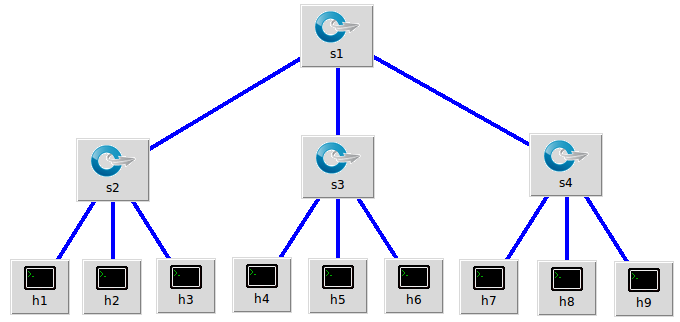
（ctrl+D命令：退出这个网络 net 查看网络状态）

（注意：没搭建一次拓扑，要输入 "mn -c"来清除剩余缓存）

输入命令：

sudo mn --topo tree,fanout=3,depth=2

3. 利用可视化工具搭建如下拓扑，并要求支持OpenFlow 1.0 1.1 1.2 1.3，设置h1（10.0.0.10）、h2（10.0.0.11）、h3（10.0.0.12），拓扑搭建完成后使用命令验证主机ip，查看拓扑端口连接情况。

（1）在~/mininet/examples目录下打开终端，执行以下命令：

./miniedit.py

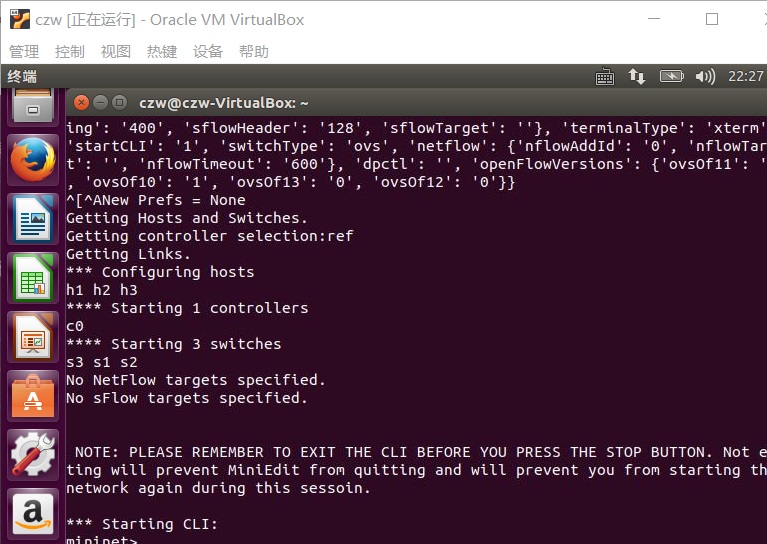
（2）接下来打开可视化工具，通过利用可视化工具，可以更加方便的的搭建拓扑、使用命令查看状态。

配置完成后，执行run

（3）通过net命令可以查看网络拓扑：

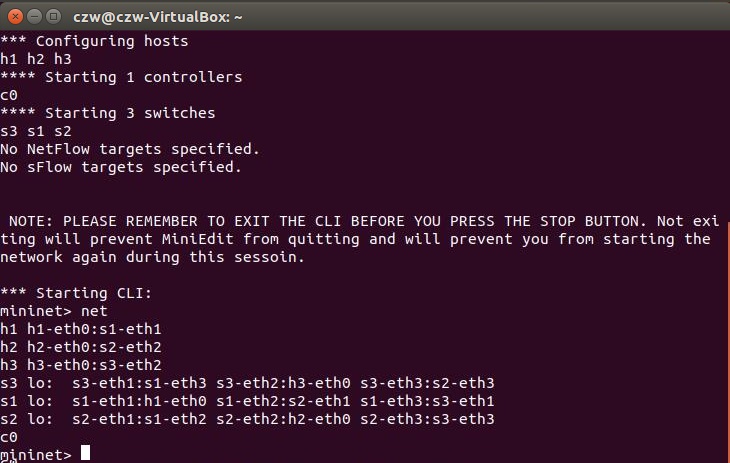
（4）使用xterm语句验证主机ip，查看各个拓扑端口连接情况:

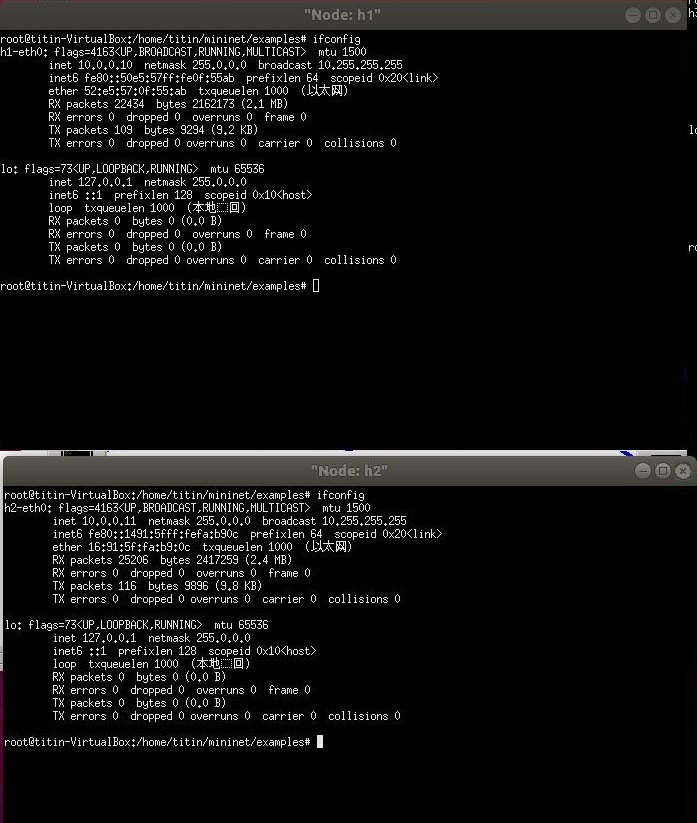
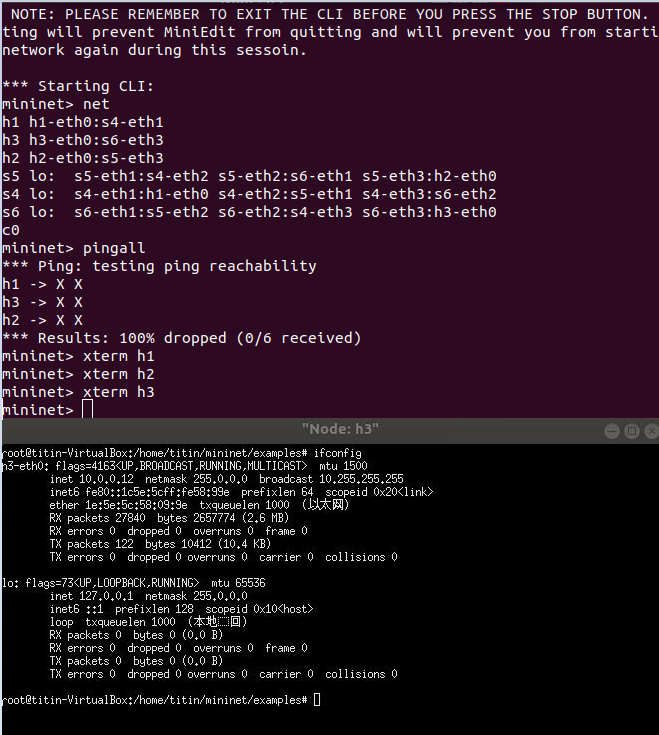
4. 利用Python脚本完成如下图所示的一个Fat-tree型的拓扑

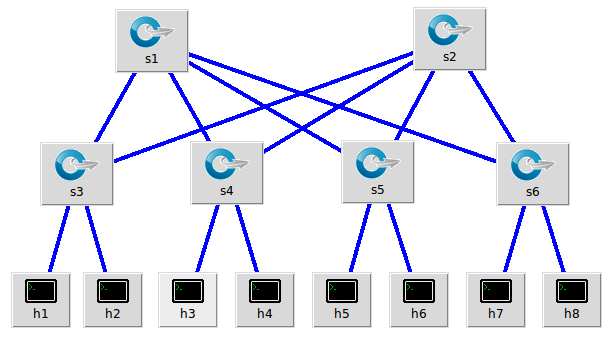
（1）python代码如下：

#!/usr/bin/python
# sudo mn --custom fattree.py --topo mytopo --switch ovsk,protocols=OpenFlow10
"""Custom topology example
Adding the 'topos' dict with a key/value pair to generate our newly defined
topology enables one to pass in '--topo=mytopo' from the command line.
"""

from mininet.topo import Topo
from mininet.net import Mininet
from mininet.node import RemoteController,CPULimitedHost
from mininet.link import TCLink
from mininet.util import dumpNodeConnections

class MyTopo(Topo):
    "Simple topology example."

    def __init__(self):
        "Create custom topo."

        # Initialize topology
        Topo.__init__(self)
        L1 = 2
        L2 = 4
        c = []
        a = []

        # add core ovs
        for i in range(L1):
                sw = self.addSwitch('s{}'.format(i+1))
                c.append(sw)

        # add aggregation ovs
        for i in range(L2):
                sw = self.addSwitch('s{}'.format(L1+i+1))
                a.append(sw)

        # add links between core and aggregation ovs
        for i in range(L1):
                sw1 = c[i]
                for sw2 in a[0: :1]:
                    self.addLink(sw2, sw1)

        #add hosts and its links with aggregation ovs
        count = 1
        for sw1 in a:
                for i in range(2):
                    host = self.addHost('h{}'.format(count))
                    self.addLink(sw1, host)
                    count += 1
topos = {'mytopo': (lambda: MyTopo())}

（2）生成拓扑：

sudo mn --custom fattree.py --topo mytopo --switch ovsk,protocols=OpenFlow10

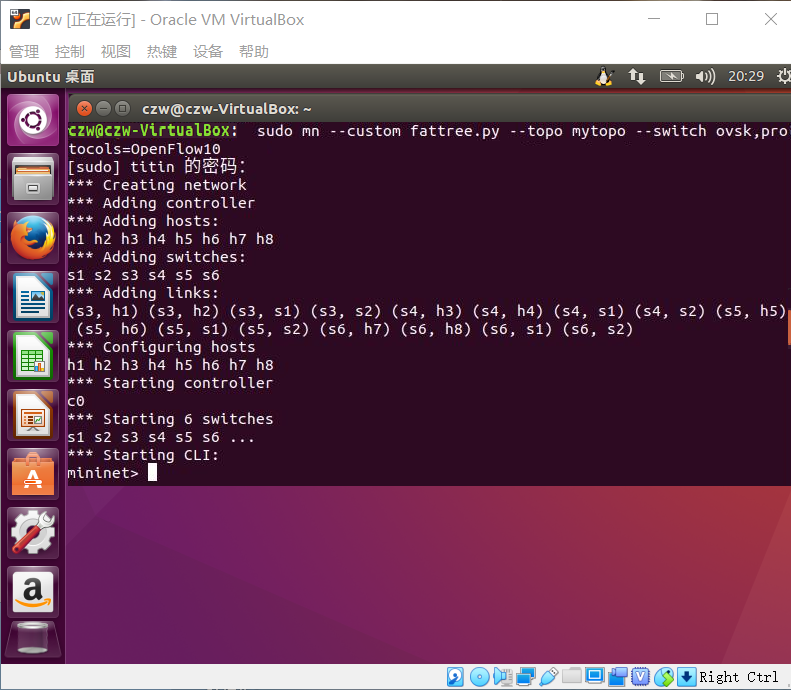
（3）使用net命令验证拓扑结构