P5173 传球

题目背景

临近中考，pG的班主任决定上一节体育课，放松一下。

题解：https://blog.csdn.net/kkkksc03/article/details/85008120

题目描述

老师带着pG的同学们一起做传球游戏。

游戏规则是这样的： nn 个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师再次吹哨子时，传球停止，此时，拿着球没有传出去的那个同学就是败者，要给大家表演一个节目。

pG提出一个有趣的问题：有多少种不同的传球方法可以使得从pG手里开始传的球，传了 mm 次以后，又回到pG手里。两种传球方法被视作不同的方法，当且仅当这两种方法中，接到球的同学按接球顺序组成的序列是不同的。比如有三个同学 11 号、 22 号、 33 号，并假设pG为 11 号，球传了 33 次回到pG手里的方式有 1 -> 2 -> 3 -> 11−>2−>3−>1和 1 -> 3 -> 2 -> 11−>3−>2−>1 ，共22 种。

输入输出格式

输入格式：
　

　

一行，有两个用空格隔开的整数 n,mn,m

　

输出格式：
　

　

11 个整数，表示符合题意的方法数。

由于答案可能过大，对10^9+7109+7取模。

　

输入输出样例

输入样例#1： 复制

3 3

输出样例#1： 复制

2

输入样例#2： 复制

30 30

输出样例#2： 复制

155117522

输入样例#3： 复制

1234 12345678

输出样例#3： 复制

424074635

说明

对于8%的数据，n \le 100,m \le 10^4n≤100,m≤104.

对于100%的数据，n \le 3500,m \le 10^9n≤3500,m≤109.

数据有一定梯度。

【题意】

n个石子堆排成一排，每次可以将连续的最少L堆，最多R堆石子合并在一起，消耗的代价为要合并的石子总数。

求合并成1堆的最小代价，如果无法做到输出0

【分析】

思路0:

TLE(8分)

    cin>>n>>m;
    f[][]=;
    for(int i=;i<=m;i++){
        for(int j=;j<n;j++){
            f[i&][j]=(f[i-&][(j-+n)%n]+f[i-&][(j+)%n])%mod;
        }
    }
    cout<<f[m&][];

思路1：

思路2:

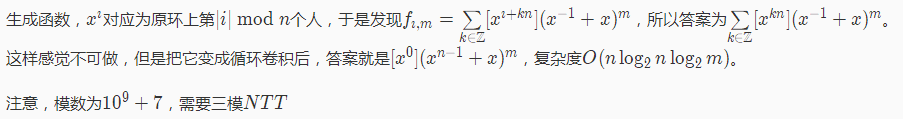
思路3:

——摘自洛谷

【代码】

思路3的

#pragma GCC optimize("Ofast,fast-math,unroll-loops")
#include<cstdio>
#include<cstring>
using namespace std;
const int N=|;
const int mod=1e9+;
int n,m,a[N],ans[N];
inline void plusx(int &x,int y){
    x+=y;if(x>=mod) x-=mod;
}
inline void PolyMul(int *a,int *b,int *c){
    int t[N];memset(t,,sizeof(int)*(n<<));
    for(int i=;i<n;i++){
        if(a[i]){
            for(int j=;j<n;j++){
                plusx(t[i+j],(long long)a[i]*b[j]%mod);
            }
        }
    }
    for(int i=;i<n;i++) c[i]=t[i];
    for(int i=n;i<n<<;i++) plusx(c[i-n],t[i]);
}
int main(){
    scanf("%d%d",&n,&m);
    a[]=a[n-]=;ans[]=;
    for(;m;m>>=,PolyMul(a,a,a)) if(m&) PolyMul(ans,a,ans);
    printf("%d",ans[]);
    return ;
}