振兴中华（dfs or dp )

小明参加了学校的趣味运动会，其中的一个项目是：跳格子。

地上画着一些格子，每个格子里写一个字，如下所示：（也可参见p1.jpg）

从我做起振
我做起振兴
做起振兴中
起振兴中华

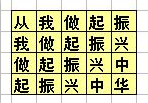
比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。

一直要跳到“华”字结束。 要求跳过的路线刚好构成“从我做起振兴中华”这句话。 请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

答案是一个整数，请通过浏览器直接提交该数字。
注意：不要提交解答过程，或其它辅助说明类的内容。

答案：35

分析：

思路一：dfs深搜

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<algorithm>
 using namespace std;

 // int dfs(int x,int y,int step){
 //     if(step==7){
 //         if(x==5&&y==4) return 1;
 //         else  return 0;
 //     }
 //     else{
 //         return dfs(x+1,y,step+1)+dfs(x,y+1,step+1);
 //     }
 // }
 int cnt=;
 void dfs(int x,int y,int step){
     if(step==){
         if(x==&&y==) cnt++;
         else return ;
     }
     else{
         dfs(x+,y,step+);
         dfs(x,y+,step+);
     }

 }

 int main(int argc, char const *argv[])
 {
     // cout<<dfs(1,1,0)<<endl;
     dfs(,,);
     cout<<cnt<<endl;
     return ;
 }

思路二：

dp思想，先说一下近似dp的思想的做法

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;

 int f(int x,int y){
     if(x==||y==) return ;/*走到边界的地方那么他就一定是一条路径，类似dp*/
     else{
         return f(x+,y)+f(x,y+);
     }
 }
 int main(int argc, char const *argv[])
 {
     cout<<f(,)<<endl;
     return ;
 }

下面是正宗dp做法：

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 int main(){
     int dp[][];
     memset(dp,,sizeof(dp));
     dp[][]=;
     for( int x=; x<=; x++ ){
         for( int y=; y<=; y++ ){
             /*[x][y]位置要么从[x-1][y]向右走，要么从[x][y-1]向下走*/
             dp[x][y]+=dp[x-][y]+dp[x][y-];
             // printf("dp[%d][%d]=%d\n",x,y,dp[x][y]);
         }
     }
     cout<<dp[][]<<endl;
     return ;
 }