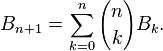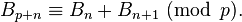贝尔数(来自维基百科)& Stirling数
贝尔数
贝尔数以埃里克·坦普尔·贝尔(Eric Temple Bell)为名,是组合数学中的一组整数数列,开首是(OEIS的A000110数列):
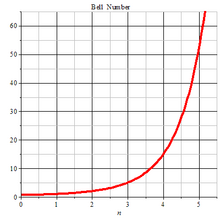
Bell Number
Bn是基数为n的集合的划分方法的数目。集合S的一个划分是定义为S的两两不相交的非空子集的族,它们的并是S。例如B3 = 5因为3个元素的集合{a, b, c}有5种不同的划分方法:
- {{a}, {b}, {c}}
- {{a}, {b, c}}
- {{b}, {a, c}}
- {{c}, {a, b}}
- {{a, b, c}};
B0是1因为空集正好有1种划分方法。空集的每个成员都是非空集合(这是Vacuous truth,因为空集实际上没有成员),而它们的并是空集本身。所以空集是它的唯一划分。
贝尔数适合递推公式:
上述组合公式的证明:
可以这样来想,B_{n+1}是含有n+1个元素集合的划分的个数,考虑元素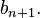
假设他被单独划分到一类,那么还剩下n个元素,这种情况下划分个数为 ;
;
假设他和某一个元素被划分为一类,那么还剩下n-1个元素,这种情况下划分个数为 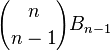 ;
;
假设他和某两个元素被划分为一类,那么还剩下n-2个元素,这种情况下划分个数为  ;
;
依次类推,得到了上述组合公式
它们也适合“Dobinski公式”:
它们也适合“Touchard同余”:若p是任意质数,那么
每个贝尔数都是"第二类Stirling数"的和
Stirling数S(n, k)是把基数为n的集划分为正好k个非空集的方法的数目。
把任一概率分布的n次矩以首n个累积量表示的多项式,其系数和正是第n个贝尔数。这种数划分的方法不像用Stirling数那个方法粗糙。
贝尔数的指数母函数是
贝尔三角形[编辑]
用以下方法建构一个三角矩阵(形式类似杨辉三角形):
- 第一行第一项是1(
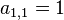 )
) - 对于n>1,第n行第一项等同第n-1行最后一项。(
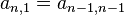 )
) - 对于m,n>1,第n行第m项等于它左边和左上方的两个数之和。(
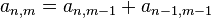 )
)
结果如下:(OEIS:A011971)
每行首项是贝尔数。每行之和是第二类Stirling数。
这个三角形称为贝尔三角形、Aitken阵列或Peirce三角形(Bell triangle, Aitken's array, Peirce triangle)。
参见[编辑]
参考[编辑]
贝尔数(来自维基百科)& Stirling数的更多相关文章
- 自然数幂和——第一类Stirling数和第二类Stirling数
第一类Stirling数 首先设 $$S_k(n)=\sum_{i=0}^ni^k$$ 根据第一类斯特林数的定义(P是排列数,C是组合数,s是Stirling) $$C_n^k={P_n^k\over ...
- arp:地址解析协议(Address Resolution Protocol)(来自维基百科)
地址解析协议(Address Resolution Protocol),其基本功能为通过目标设备的IP地址,查询目标设备的MAC地址,以保证通信的顺利进行。它是IPv4中网络层必不可少的协议,不过在I ...
- web框架--来自维基百科
- Bell(hdu4767+矩阵+中国剩余定理+bell数+Stirling数+欧几里德)
Bell Time Limit:3000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Submit Status ...
- 第一类和第二类Stirling数
做了老是忘…… 实际问题: 找维基百科.百度百科…… 第一类Stirling数 n个元素构成m个圆排列 S(n,m)=S(n-1,m-1)+(n-1)*S(n-1,m) 初始 S(0,0)=1 S(n ...
- [总结] 第二类Stirling数
上一道例题 我们来介绍第二类Stirling数 定义 第二类Stirling数实际上是集合的一个拆分,表示将n个不同的元素拆分成m个集合的方案数,记为 或者 .和第一类Stirling数不同的是,集合 ...
- Stirling数
第一类: 定义 第一类Stirling数表示表示将 n 个不同元素构成m个圆排列的数目.又根据正负性分为无符号第一类Stirling数 和带符号第一类Stirling数 .有无符号Stir ...
- Bell数和Stirling数
前面说到了Catalan数,现在来了一个Bell数和Stirling数.什么是Bell数,什么是Stirling数呢?两者的关系如何,有用于解决什么算法问题呢? Bell数是以Bell这个人命名的,组 ...
- Stirling数入门
第一类Stirling数 定义 $$\begin{aligned}(x)_n & =x(x-1)...(x-n+1)\\&= s(n, 0) + s(n,1)x +..+s(n,n)x ...
随机推荐
- oracle基础函数--decode
含义解释:decode(条件,值1,返回值1,值2,返回值2,...值n,返回值n,缺省值) 该函数的含义如下:IF 条件=值1 THEN RETURN(翻译值1)ELSIF 条件=值2 THEN R ...
- MySQL与SQL语句的操作
MySQL与SQL语句的操作 Mysql比较轻量化,企业用的是Oracle,基本的是熟悉对数据库,数据表,字段,记录的更新与修改 1. mysql基本信息 特殊数据库:information_sche ...
- Xcode8.0 / OS X EI Capitan 10.11.6 提交报错90111
改用新系统和新版xcode(都是正式版)后,提交App Store审核时报错: INFO ITMS-90111: "Beta Toolchain. 构建新的 App 和App 更新时,必须使 ...
- Windows 系统里面的 hosts 文件
一.什么是hosts文件? hosts文件是一个用于储存计算机网络中各节点信息的计算机文件.这个文件负责将主机名映射到相应的IP地址.hosts文件通常用于补充或取代网络中DNS的功能.和DNS不同的 ...
- [CocoaPods]常见问题
“现在Swift有一个内置的包管理器,CocoaPods会停止开发吗?” Swift Package Manager(SPM)处于“早期设计和开发”阶段[1].它目前不支持iOS,观看操作系统或Obj ...
- Testing - 软件测试知识梳理 - 软件性能测试
软件性能测试的基本概念 软件的性能是软件的一种非功能特性,它关注的不是软件是否能够完成特定的功能,而是软件在完成该功能时展示出来的及时性. 软件性能的指标 响应时间:是指系统对请求作出响应的时间,并且 ...
- Hbase shell基本操作
1.启动cd <hbase_home>/bin$ ./start-hbase.sh 2.启动hbase shell # find hadoop-hbase dfs fileshadoop ...
- Mac下命令行批量重命名
日常中碰到需要批量修改文件名怎么办?嗯,来终端先 案例:将Users/case目录下所有html文件修改为php文件 步骤: 1.进入目标文件夹 $ cd Users/case 2.执行以下命令 $ ...
- Kaggle项目实战一:Titanic: Machine Learning from Disaster
项目地址 https://www.kaggle.com/c/titanic 项目介绍: 除了乘客的编号以外,还包括下表中10个字段,构成了数据的所有特征 Variable Definition Key ...
- 第六章:四大组件之Activity
tivityActivity作为Android四大组件之一,也是其中最重要的一个组件.作为一个与用户交互的组件,我们可以把Activity比较成为windows系统上的一个文件夹窗口,是一个与用户交互 ...