C4.5决策树--Java

ID3是以信息增益作为划分训练数据集的特征，即认为信息增益大的特征是对分类结果影响更大，但是信息增益的方法偏向于选择取值较多的特征，因此引入了C4.5决策树，也就是使用信息增益率(比)来作为划分数据集的特征，信息增益率定义如下：

。

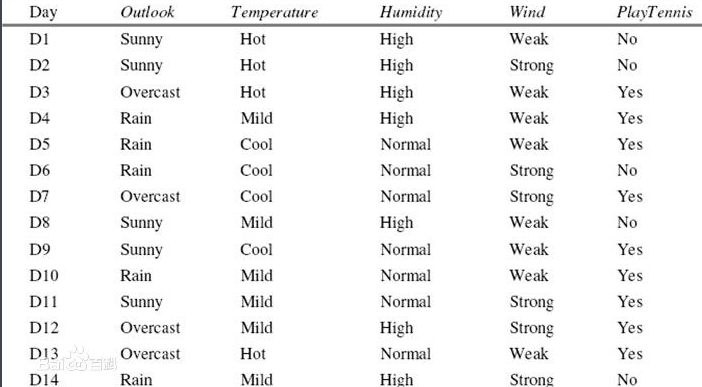
就是在ID3中已经计算出特征A的信息增益之后再除一个熵H_A(D),H_A(D)的计算例子如下图所示：

，

对应的数据集是：

例子来自：http://baike.baidu.com/link?url=uVS7uFMB44R86TEdRzwwpNWsmzQtA3ds88X0CLYLN0C-8bmS-OAlOFnpD8PNv6pdD_SvWOIpV8UMKQRpVu4tHK

以下是代码实现：

//import java.awt.color.ICC_ColorSpace;
import java.io.*;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.HashMap;
import java.util.HashSet;
import java.util.Iterator;
//import java.util.Iterator;
import java.util.List;
//import java.util.Locale.Category;
import java.util.Map;
import java.util.Map.Entry;
import java.util.Set;
class decisionTree{
 
    private static Map<String, Map<String, Integer>> featureValuesAndCounts=new HashMap<String, Map<String,Integer>>();
    private static ArrayList<String[]> dataSet=new ArrayList<String[]>();
    private static ArrayList<String> features=new ArrayList<String>();
    private static Set<String> category=new HashSet<String>();
    //public static DecisionNode root=new DecisionNode();
    //private static  ArrayList<ArrayList<String>> featureValue=new ArrayList<ArrayList<String>>();
    public static void GetDataSet()
    {
        File file = new File("C:\\Users\\hfz\\workspace\\decisionTree\\src\\loan.txt");
        try{
            BufferedReader br = new BufferedReader(new FileReader(file));//
            String s = null;
            s=br.readLine();//读取第一行的内容，即是各特征的名称
            String[] tempFeatures=s.split(",");
            for (String string1 : tempFeatures) {
                features.add(string1);
            }
            s=br.readLine();        //开始读取特征值
            String[] tt=null;
            int flag=s.length();
            while(flag!=0){//英文文档读到结尾得到的值是null，而中文文档读到结尾得到的值却是""
                tt=s.split(",");
                dataSet.add(tt);    //将特征值存入
                category.add(tt[tt.length-1]);//category为集合类型，用于存储类型值
 
                s=br.readLine();
                if (s!=null) {
                    flag = s.length();
                }
                else{
                    flag=0;
                }
 
            }
 
            for (int j = 0; j < features.size(); j++) {//逻辑上模拟列优先的方式读取二维数组形式的数据集，就是首先读取一个特征名称，再遍历数据集
                Map<String, Integer> ttt=new HashMap<String, Integer>();//将某特征的各个特征值存入Map中，然后再度第二个特征，再遍历数据集。。。
                for (int i = 0; i < dataSet.size(); i++) {
                    String currentFeatureValue=dataSet.get(i)[j];
                    if(!(ttt.containsKey(currentFeatureValue)))
                        ttt.put(currentFeatureValue, 1);
                    else {
                        ttt.replace(currentFeatureValue, ttt.get(currentFeatureValue)+1);
                    }
 
                }
                featureValuesAndCounts.put(features.get(j), ttt);//嵌套形式的Map，第一层的key是特征名称，value是一个新的Map
                // 新Map中key是特征的各个值，value是特征值在数据集中出现的次数。
 
            }
 
            br.close();
        }
 
        catch(Exception e){
            e.printStackTrace();
        }
    }
    public static DecisionNode treeGrowth(ArrayList<String[]> dataset,String currentFeatureName,
                                          String currentFeatureValue,ArrayList<String> current_features,
                                          Map<String,Map<String,Integer>> current_featureValuesCounts){
        /*
        dataset:用于split方法，从dataset数据集中去除掉具有某个特征值的对应的若干实例，生成一个新的新的数据集
        currentFeatureName:当前的特征名称，用于叶子节点，赋值给叶子节点的featureName字段
        currentFeatureValue：当前特征名称对应的特征值，也用于叶子节点，赋值给featureValue字段
        current_features:当前数据集中包含的所有特征名称，用于findBestAttribute方法，找到信息增益最大的的属性
        current_featureValuesCounts:当前数据集中所有特征的各个特征值出现的次数，用于findBestAttribute方法，用于计算条件熵，进而计算信息增益。
         */
        ArrayList<String> classList=new ArrayList<String>();
        int flag=0;
        for (String[] string : dataset) {
            //测试数据集中类型值的数量,flag表示数据集中的类型数量
            if (classList.contains(string[string.length-1])) {
 
            }
            else {
                classList.add(string[string.length-1]);
                flag++;//如果flag>1表示数据集
            }
 
        }
        if(1==flag){//如果只有一个类结果，则返回此叶子节点
            DecisionNode d=new DecisionNode();
            d.init(currentFeatureName,classList.get(0),currentFeatureValue);
            return d;
        }
        if (dataset.get(0).length==1) {//如果数据集已经没有属性了只剩下类结果，则返回占比最大的类结果，也是叶子节点
            DecisionNode d=new DecisionNode();
            d.init(currentFeatureName,classify(classList),currentFeatureValue);
            return d;
        }
 
        /*
        DecisionNode是一个自定义的递归型的数据类型，类中一个children字段是DecisionNode类型的数组，
        正好用这种类型来存储递归算法产生的结果(决策树)，也就是用这种结构来存储一棵树。
        */
        //程序运行到这里就说明此节点不是叶子节点
        DecisionNode root2=new DecisionNode();//那么root2就是一个决策属性节点(非叶子节点)了，非叶子节点就有孩子节点，下面就是计算它的孩子节点
 
        int bestFeatureIndex=findBestAttribute(dataset,current_features,current_featureValuesCounts);
        String bestFeatureLabel=current_features.get(bestFeatureIndex);
        //root.testCondition=bestFeatureLabel;
        ArrayList<String> feature_values=new ArrayList<String>();
        for (Entry<String, Integer> featureEntry : current_featureValuesCounts.get(bestFeatureLabel).entrySet()) {
            feature_values.add(featureEntry.getKey());
 
        }
        //给非叶子节点，也就是特征节点仅仅赋特征名称值
        root2.init(currentFeatureName,currentFeatureValue);//java中不能是使用像C++中默认参数的函数，只能通过重载来实现同样的目的。
        for (String values : feature_values) {
            //DecisionNode tempRoot=new DecisionNode();
 
            ArrayList<String[]> subDataSet = splitDataSet(dataset, bestFeatureIndex, values);//生成子数据集，即去除了包含values的实例，
            // 接下来就是计算对此数据集利用决策树进行决策，又需要调用treeGrow方法
            //所以，接下来需要得到对应这个子数据集的特征名称以及每个特征值在数据集中出现的次数
            ArrayList<String> currentAttibutes=new ArrayList<>();
            Iterator item1=current_features.iterator();
            while(item1.hasNext()){
                currentAttibutes.add(item1.next().toString());//这个子数据集的特征名称
            }
 
            Map<String,Map<String,Integer>> currentAttributeValuesCounts=new HashMap<String, Map<String, Integer>>();
            //ArrayList<String[]> subDataSet = splitDataSet(dataset, bestFeatureIndex, values);
            currentAttibutes.remove(bestFeatureLabel);
            for (int j = 0; j < currentAttibutes.size(); j++) {
                Map<String, Integer> ttt=new HashMap<String, Integer>();
                for (int i = 0; i <subDataSet.size(); i++) {
                    String currentFeatureValueXX=subDataSet.get(i)[j];
                    if(!(ttt.containsKey(currentFeatureValueXX)))
                        ttt.put(currentFeatureValueXX, 1);
                    else {
                        ttt.replace(currentFeatureValueXX, ttt.get(currentFeatureValueXX)+1);
                    }
 
                }
                currentAttributeValuesCounts.put(currentAttibutes.get(j), ttt);//每个特征值在数据集中出现的次数
 
            }
 
            root2.add(treeGrowth(subDataSet, bestFeatureLabel, values, currentAttibutes, currentAttributeValuesCounts));
 
        }
 
        return root2;
 
    }
 
    public static void main(String[] agrs){
        decisionTree.GetDataSet();
        DecisionNode dd=decisionTree.treeGrowth(dataSet,"oo","xx",features,featureValuesAndCounts);
        System.out.print(dd);
 
    }
 
    public static double calEntropy(ArrayList<String[]> dataset){//熵表示随机变量X不确定性的度量，在决策树中计算的熵就是决策结果这个变量的熵。
        int sampleCounts=dataset.size();
        Map<String, Integer> categoryCounts=new HashMap<String, Integer>();
        for (String[] strings : dataset) {
 
            if(categoryCounts.containsKey(strings[strings.length-1]))
                categoryCounts.replace(strings[strings.length-1], categoryCounts.get(strings[strings.length-1])+1);
            else {
                categoryCounts.put(strings[strings.length-1],1);
            }
 
        }
        double shannonEnt=0.0;
        for (Integer value: categoryCounts.values()) {
            double probability=value.doubleValue()/sampleCounts;
            shannonEnt-=probability*(Math.log10(probability)/Math.log10(2));
 
        }
        return shannonEnt;
    }
 
    public static  int findBestAttribute(ArrayList<String[]> dataset,ArrayList<String> currentFeatures,
                                         Map<String,Map<String,Integer>> currentFeatureValuesCounts){
        double baseEntroy=calEntropy(dataset);//计算基础熵，就是在不划分出某个特征的情况下。
        double bestInfoGain=0.0;
        int bestFeatureIndex=-1;
 
        for (int i = 0; i <currentFeatures.size(); i++) {//遍历当前数据集的每个特征，计算每个特征的信息增益
            double conditionalEntroy=0.0;
            double entroy=0.0;
            Map<String,Integer> tempFeatureCounts=currentFeatureValuesCounts.get(currentFeatures.get(i));
            //Map类型有一个entrySet方法，此方法返回一个Map.Entry类型的集合，其中集合中的每个元素就是一个键值对，利用增强型的for循环可以遍历Map中
            //key(entry.getkey)和value(entry.getValue)
            for (Entry<String, Integer> entry : tempFeatureCounts.entrySet()) {
                //计算条件熵，就是根据某个具体特征值划分出新的数据集，计算新的数据集的基础熵，再乘以权值，累加得到某个特征的条件熵。
                conditionalEntroy+=(entry.getValue().doubleValue()/dataset.size())*calEntropy(splitDataSet(dataset, i, entry.getKey()));
                //根据信息增益进一步计算信息增益比
                double tempValue=entry.getValue().doubleValue()/dataset.size();
                entroy+=tempValue*(Math.log10(tempValue)/Math.log10(2));
 
            }
 
            if ((baseEntroy-conditionalEntroy)/(-entroy)>bestInfoGain) {
                bestInfoGain=(baseEntroy-conditionalEntroy)/(-entroy);
                bestFeatureIndex=i;
 
            }
        }
        if (-1==bestFeatureIndex){
            System.out.print("cannot find best attribute!");
            return -1;
        }
        else {
            return bestFeatureIndex;//返回信息增益最大的特征的索引，在当前特征(currentFeatures)中的索引。
        }
    }
    public static String classify(ArrayList<String> dataset) {
 
        Map<String, Integer> categoryCount = new HashMap<String, Integer>();
        for (String s1 : dataset) {
            if (categoryCount.containsKey(s1)) {
                categoryCount.replace(s1, categoryCount.get(s1) + 1);
            } else {
                categoryCount.put(s1, 1);
            }
        }
        int maxCounts=-1;
        String maxCountsCategory=null;
        for (Entry<String,Integer> entry:categoryCount.entrySet()){//利用Map.Entry得到Map中的Value最大的键值对。
            if (entry.getValue()>maxCounts){
                maxCounts=entry.getValue();
                maxCountsCategory=entry.getKey();
            }
        }
        return  maxCountsCategory;
 
    }
 
    public static ArrayList<String[]> splitDataSet(ArrayList<String[]> dataset,int featureIndex,String featureValue
    ){
        ArrayList<String[]> tempDataSet=new ArrayList<String[]>();
        for (String[] strings : dataset) {
            if (strings[featureIndex].equals(featureValue)) {
 
                String[] xx=strings.clone();//数组的clone方法实现的是浅拷贝，实质就是以下的过程
                /*
                for (int i = featureIndex; i < strings.length-1; i++) {
                    xx[i]=strings[i];//就是把引用的值(地址)复制了一份，指向了同一个对象。
                }
 
                */
                for (int i = featureIndex; i < strings.length-1; i++) {//xx中各个元素的值与strings中各个元素的值完全相等。
                    xx[i]=xx[i+1];//只是复制了引用的值而已，跟引用指向的对象没一点关系。Java将基本类型和引用类型变量都看成是值而已·
                }
                //最最最需要注意的一点，以上代码不能以下面这种形式实现
                /*
                for (int i = featureIndex; i < strings.length-1; i++) {//
                    strings[i]=strings[i+1];//这样会改变strings指向的对象，进而影响到dataset，改变了函数的参数dataset，
                    这样就在函数内“无意间”修改了dataset的值，集合类型，其实所有引用类型都是，以参数形式传入函数的话，可能会“无意间”就被修改了
                }
                 */
                String[] tempStrings=new String[xx.length-1];
                for (int i = 0; i < tempStrings.length; i++) {
                    tempStrings[i]=xx[i];
 
                }
                tempDataSet.add(tempStrings);
            }
 
        }
        return tempDataSet;
    }
 
}
class DecisionNode{
    public String featureName;
    public String result;
    public String featureValue;
    public List<DecisionNode> children=new ArrayList<DecisionNode>();
    public void add(DecisionNode node){
        children.add(node);
    }
    public void init(String featureName,String result,String featureValue){
        this.featureName=featureName;
        this.result=result;
        this.featureValue=featureValue;
    }
    public void init(String featureName,String featureValue){
        this.featureName=featureName;
        this.featureValue=featureValue;
    }
}