POJ 2549

Sumsets

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 8235		Accepted: 2260

Description

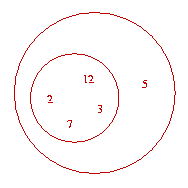Given S, a set of integers, find the largest d such that a + b + c = d where a, b, c, and d are distinct elements of S.

Input

Several S, each consisting of a line containing an integer 1 <= n <= 1000 indicating the number of elements in S, followed by the elements of S, one per line. Each element of S is a distinct integer between -536870912 and +536870911 inclusive. The last line of input contains 0.

Output

For each S, a single line containing d, or a single line containing "no solution".

Sample Input

5
2
3
5
7
12
5
2
16
64
256
1024
0

Sample Output

12
no solution

Source

Waterloo local 2001.06.02

 

分成a + b  和 d - c两个集合

x = d - c    保存a + b 的所有值，二分查找x并判断合理性

 

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>

 using namespace std;

 struct node { int v,a,b; };
 const int MAX = ;
 int N,len = ;
 int ele[MAX];
 node y[MAX * MAX];

 bool cmp(node a,node b) { return a.v < b.v; }

 bool solve() {
         for(int i = N - ; i >= ; --i) {
                 for(int j = N - ; j >= ; --j) {
                         if(i == j) continue;
                         int d = ele[i] - ele[j];
                        // printf("ele = %d d = %d\n",ele[i],d);
                         int l = ,r = len - ;
                         while(l < r) {
                                 int mid = (l + r + ) >> ;
                                 if(y[mid].v > d) r = mid - ;
                                 else l = mid;
                         }
                         if(y[l].v == d) {
                                 for(int k = l; k < len; ++k) {
                                         if(y[k].v == d && y[k].a != ele[j] && y[k].b != ele[j]
                                            && y[k].a != ele[i] && y[k].b != ele[i]) {
                                                 printf("%d\n",ele[i]);
                                                 return true;
                                         }
                                 }
                                 for(int k = l; k >= ; --k) {
                                         if(y[k].v == d && y[k].a != ele[j] && y[k].b != ele[j]
                                            && y[k].a != ele[i] && y[k].b != ele[i]) {
                                                 printf("%d\n",ele[i]);
                                                 return true;
                                         }

                                 }

                         }

                 }
         }

         return false;

 }

 int main()
 {
    // freopen("sw.in","r",stdin);

     while(~scanf("%d",&N) && N ) {
             for(int i = ; i < N; ++i) scanf("%d",&ele[i]);

             sort(ele,ele + N);
             N = unique(ele,ele + N) - ele;

             len = ;
             for(int i = ; i < N; ++i) {
                     for(int j = i + ; j < N; ++j) {
                             y[len].v = ele[i] + ele[j];
                             y[len].a = ele[i];
                             y[len++].b = ele[j];
                     }
             }

             sort(y,y + len,cmp);

             if(!solve()) printf("no solution\n");
     }
     return ;
 }