P1886 滑动窗口&&P1440 求m区间内的最小值

声明：下面这两个题就不要暴力了，学一学单调队列吧

　　推荐博文：https://www.cnblogs.com/tham/p/8038828.html

单调队列入门题

P1440 求m区间内的最小值

题目描述

一个含有n项的数列(n<=2000000)，求出每一项前的m个数到它这个区间内的最小值。若前面的数不足m项则从第1个数开始，若前面没有数则输出0。

输入输出格式

输入格式：

第一行两个数n，m。

第二行，n个正整数，为所给定的数列。

输出格式：

n行，第i行的一个数ai，为所求序列中第i个数前m个数的最小值。

输入输出样例

输入样例#1： 复制

6 2
7 8 1 4 3 2

输出样例#1： 复制

0
7
7
1
1
3

说明

【数据规模】

m≤n≤2000000

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define N 5000050
using namespace std;

void in(int &x){
    register char c=getchar();x=;int f=;
    while(!isdigit(c)){if(c=='-') f=-;c=getchar();}
    while(isdigit(c)){x=x*+c-'';c=getchar();}
    x*=f;
}

struct node{
    int x,id;
}mx[N],mi[N];
int hx,tx,hi,ti,n,m,anx[N],ani[N];
int main()
{
    in(n);in(m);
    hx=hi=;tx=ti=;
    for(int i=,x;i<=n;i++){
        in(x);
        while(hx<=tx&&x>=mx[tx].x) --tx;
        mx[++tx].x=x;mx[tx].id=i;
        while(mx[hx].id<=i-m) ++hx;

        while(hi<=ti&&x<=mi[ti].x) --ti;
        mi[++ti].x=x;mi[ti].id=i;
        while(mi[hi].id<=i-m) ++hi;

        if(i>=m) anx[i]=mx[hx].x,ani[i]=mi[hi].x;
    }for(int i=m;i<=n;i++) printf("%d ",ani[i]);
    puts("");
    for(int i=m;i<=n;i++) printf("%d ",anx[i]);
    return ;
}

P1886 滑动窗口

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

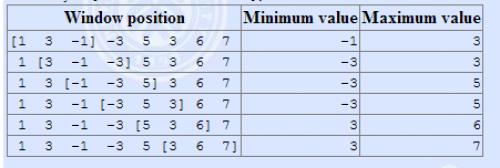
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

输入输出样例

输入样例#1： 复制

8 3
1 3 -1 -3 5 3 6 7

输出样例#1： 复制

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

#include<bits/stdc++.h>

#define N 2000005
using namespace std;

void in(int &x){
    register char c=getchar();x=;int f=;
    while(!isdigit(c)){if(c=='-') f=-;c=getchar();}
    while(isdigit(c)){x=x*+c-'';c=getchar();}
    x*=f;
}

int n,m,q[N],a[N],ans[N];
int main()
{
    in(n);in(m);
    int head=,tail=;
    for(int i=;i<=n;i++){
        in(a[i]);
        while(head<=tail&&a[q[tail]]>=a[i]) --tail;
        q[++tail]=i;
        while(q[head]<=i-m) ++head;
        ans[i]=a[q[head]];
    }for(int i=;i<=n;i++) printf("%d\n",ans[i-]);
    return ;
}