【知识总结】卡特兰数 (Catalan Number) 公式的推导

卡特兰数的英文维基讲得非常全面，强烈建议阅读！

Catalan number - Wikipedia

(本文中图片也来源于这个页面)
由于本人太菜，这里只选取其中两个公式进行总结。
（似乎就是这两个比较常用？）
首先先扔卡特兰数的定义式

\[Catalan_n=\prod_{i=1}^{n-1}Catalan_i*Catalan_{n-i}\]

(卡特兰数的很多应用，比如二叉树形态数，出栈序列数等，都由这个定义式得到。详见英文维基)

公式1 (通项公式) ：

\[Catalan_n=\frac{1}{n+1}C_{2n}^n\]

在上文提到的出栈序列的问题情景中，如果有\(n\)个元素，在平面直角坐标系中用\(x\)坐标表示入栈数，\(y\)坐标表示出栈数，则坐标\((a,b)\)表示目前已经进行了\(a\)次入栈和\(b\)次出栈，则再进行一次入栈就是走到\((a+1,b)\)，再进行一次出栈就是走到\((a,b+1)\)。并且，由于入栈数一定小于等于出栈数，所以路径不能跨越直线\(y=x\)
因此，题目相当于求从\((0,0)\)走到\((n,n)\)且不跨越直线\(y=x\)的方案数
首先，如果不考虑不能跨越直线\(y=x\)的要求，相当于从\(2n\)次操作中选\(n\)次进行入栈，则方案数为\(C_{2n}^n\)。
然后，考虑对于一种不合法的方案，一定在若干次操作后有一次出栈数比入栈数多一次，这个点在直线\(y=x+1\) (即下图中红色的线) 上。那么把第一次碰到该直线以后的部分关于该直线对称，则最终到达的点是\((n-1,n+1)\) (如下图) 。

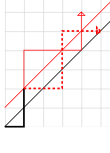
图源：英文维基 (即文首网址)
显然，任何非法方案都可以通过此方式变成一条从\((0,0)\)到\((n-1,n+1)\)的路径，有\(C_{2n}^{n+1}\)种。而任何合法方案由于不接触直线\(y=x+1\)，无论从哪个点对称都不是一条连续的路径。由于合法方案数就是\(Catalan_n\)，所以：

\[
\begin{aligned}
Catalan_n&=C_{2n}^n-C_{2n}^{n+1}\\
&=\frac{(2n)!}{n!*n!}-\frac{(2n)!}{(n+1)!*(n-1)!}\\
&=\frac{1}{n+1}(\frac{(2n)!*(n+1)}{n!*n!}-\frac{(2n)!}{n!*(n-1)!})\\
&=\frac{1}{n+1}(\frac{(2n)!*(n+1)}{n!*n!}-\frac{(2n)!*n}{n!*n!})\\
&=\frac{1}{n+1}*\frac{(2n)!*(n+1)-(2n)!*n}{n!*n!}\\
&=\frac{1}{n+1}*\frac{(2n)!}{n!*n!}\\
&=\frac{1}{n+1}C_{2n}^n\\
\end{aligned}
\]

公式2 (递推公式) ：

\[Catalan_{n+1}=\frac{4n+2}{n+2}Catalan_n\]

(这个公式的推导过程似乎网上没有，估计是思路太简单了……我太菜了想了半天才推出来)
由上面那个通项公式得

\[
\begin{aligned}
Catalan_{n+1}&=\frac{1}{n+2}C_{2n+2}^{n+1}\\
&=\frac{1}{n+2}*\frac{(2n+2)!}{(n+1)!*(n+1)!}\\
&=\frac{1}{n+2}*\frac{(2n)!*(2n+1)*(2n+2)}{n!*n!*(n+1)^2}\\
&=\frac{1}{n+2}*\frac{(2n+1)*(2n+2)}{(n+1)}*\frac{1}{n+1}*\frac{(2n)!}{n!*n!}\\
&=\frac{2(2n+1)}{n+2}*\frac{1}{n+1}*C_{2n}^n\\
&=\frac{4n+2}{n+2}Catalan_n\\
\end{aligned}
\]