hihocoder #1034 : 毁灭者问题 平衡树（set）+线段树

#1034 : 毁灭者问题

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在 Warcraft III 之冰封王座中，毁灭者是不死族打三本后期时的一个魔法飞行单位。

毁灭者的核心技能之一，叫做魔法吸收（Absorb Mana）：

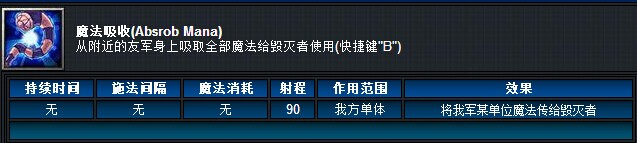
现在让我们来考虑下面的问题：

假设你拥有 n 个魔法单位，他们从左到有站在一行，编号从 1 到 n。 每个单位拥有三项属性：

• si: 初始法力。

• mi: 最大法力上限。

• ri: 每秒中法力回复速度。

现在你操纵一个毁灭者，有 m 个操作，t l r，表示时刻 t，毁灭者对所有编号从 l 到 r 的单位，使用了魔法吸收。操作按照时间顺序给出，计算毁灭者一共吸收了多少法力。

输入

输入数据的第一行有一个整数 n(1 ≤  n ≤105) — 你的魔法单位的数目。

接下来的 n 行，每行有三个整数 si, mi, ri(0 ≤ si ≤ mi ≤ 105, 0 ≤ ri ≤ 105) 描述一个魔法单位。

接下来一行又一个整数 m(1 ≤ m ≤ 105)， — 操作的数目。

接下来的 m 行，每行描述一个操作 t, l, r(0 ≤ t ≤ 109, 1 ≤ l ≤ r ≤ n)，t 非降。

输出

输出一行一个整数表示毁灭者一共吸收了多少法力。

样例输入

5
0 10 1
0 12 1
0 20 1
0 12 1
0 10 1
2
5 1 5
19 1 5

样例输出

　　　　83

题解：

　　　　自己写了一棵线段树的做法，看了网上一篇辣鸡博客，哎，无语了，

　　　　自己写的时候是知道的这个写法比暴力还暴力，n^2logn的，但是还是

　　　　写了，结果TLE，T飞了。

附上T飞代码

 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<iostream>
 #include<cstdio>
 
 #define N 100007
 #define ll long long
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if (ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }
 
 int n,m;
 ll ans;
 struct Node
 {
     ll t,m,r,s;
 }tr[N*];
 
 inline void update(int p)
 {
     tr[p].s=tr[p<<].s+tr[p<<|].s;
 }
 void build(int p,int l,int r)
 {
     if (l==r)
     {
         tr[p].s=read(),tr[p].m=read(),tr[p].r=read();
         tr[p].t=;
         return;
     }
     int mid=(l+r)>>;
     build(p<<,l,mid),build(p<<|,mid+,r);
     update(p);
 }
 void renew(int p,int l,int r,int x,int y,int t)
 {
     if (l==r)
     {
         if (tr[p].s+(t-tr[p].t)*tr[p].r>tr[p].m) tr[p].s=tr[p].m;
         else tr[p].s+=(t-tr[p].t)*tr[p].r;
         tr[p].t=t;
         return;
     }
     int mid=(l+r)>>;
     if (y<=mid) renew(p<<,l,mid,x,y,t);
     else if (x>mid) renew(p<<|,mid+,r,x,y,t);
     else renew(p<<,l,mid,x,mid,t),renew(p<<|,mid+,r,mid+,y,t);
     update(p);
 }
 ll query(int p,int l,int r,int x,int y)
 {
     if (l==x&&y==r) return tr[p].s;
     int mid=(l+r)>>;
     if (y<=mid) return query(p<<,l,mid,x,y);
     else if (x>mid) return query(p<<|,mid+,r,x,y);
     else return query(p<<,l,mid,x,mid)+query(p<<|,mid+,r,mid+,y);
 }
 void clean_all(int p,int l,int r,int x,int y)
 {
     if (l==r)
     {
         tr[p].s=;
         return;
     }
     int mid=(l+r)>>;
     if (y<=mid) return clean_all(p<<,l,mid,x,y);
     else if (x>mid) return clean_all(p<<|,mid+,r,x,y);
     else clean_all(p<<,l,mid,x,mid),clean_all(p<<|,mid+,r,mid+,y);
     update(p);
 }
 int main()
 {
     freopen("fzy.in","r",stdin);
     freopen("fzy.out","w",stdout);
 
     n=read(),build(,,n);
     m=read();
     for (int i=;i<=m;i++)
     {
         int t=read(),x=read(),y=read();
         renew(,,n,x,y,t);
         ans+=query(,,n,x,y);
         clean_all(,,n,x,y);
     }
     printf("%lld",ans);
 }

　　　　正解思路

　　　　对于s,m,r我们可以这样想，

　　　　对于输入的间隔tk-tk-1，设为d，如果d*r>m 则为m　1

　　　　　　　　　　　　　　　　　  如果d*r<=m，则为r*d    2

　　　　所以答案就等于所以人，满足1的个数乘以m，以及满足2的∑di  *r，这个就是答案。

　　　　

　　　　我们应该对于每个人来计算答案，对于每个人，如果暴力计算的话，就是O（nm）对吧。

　　　　还是T飞，那怎么办呢，可以用一棵平衡树+线段树来维护，对于每个起始时间，结束时间

　　　　都放入平衡树中，间隔即为判断条件，可以放入线段树中，结束时间时在维护，一下，删除

　　　　所以，每个询问只会被插入一次，删除一次，对于每个人询问一次，所以总复杂度为O（nlgn）。

　　　　代码，莫名wrong，但是对拍没有错，就精神ac吧。

 #include<cstring>
 #include<cmath>
 #include<algorithm>
 #include<cstdio>
 #include<iostream>
 #include<set>
 #include<vector>
 
 #define lson tr[p].ls
 #define rson tr[p].rs
 #define z1 set<int>::iterator
 #define N 100007
 #define ll long long
 using namespace std;
 inline int read()
 {
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if (ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
     return x*f;
 }
 
 int n,m,root,sz;
 ll ans;
 vector<int>hd[N],ed[N];
 set<int>q;//哪几个时间段有
 struct Node
 {
     ll s,m,r;
 }a[N];
 struct Date
 {
     int num,sum,ls,rs;
 }tr[];
 
 inline void update(int p)
 {
     tr[p].sum=tr[lson].sum+tr[rson].sum;
     tr[p].num=tr[lson].num+tr[rson].num;
 }
 void add(int &p,int l,int r,int x,int flag)
 {
     if(!p) p=++sz;
     if (l==r)
     {
         tr[p].sum+=x*flag,tr[p].num+=flag;
         return;
     }
     int mid=(l+r)>>;
     if (x<=mid) add(lson,l,mid,x,flag);
     else add(rson,mid+,r,x,flag);
     update(p);
 }
 ll query1(int p,int l,int r,int x,int y)
 {
     if (!p) return ;
     if (l==x&&r==y) return tr[p].sum;
     int mid=(l+r)>>;
     if (y<=mid) return query1(lson,l,mid,x,y);
     else if (x>mid) return query1(rson,mid+,r,x,y);
     else return query1(lson,l,mid,x,mid)+query1(rson,mid+,r,mid+,y);
 }
 ll query2(int p,int l,int r,int x,int y)
 {
     if (!p) return ;
     if (l==x&&r==y) return tr[p].num;
     int mid=(l+r)>>;
     if (y<=mid) return query2(lson,l,mid,x,y);
     else if (x>mid) return query2(rson,mid+,r,x,y);
     else return query2(lson,l,mid,x,mid)+query2(rson,mid+,r,mid+,y);
 }
 int main()
 {
     freopen("fzy.in","r",stdin);
     freopen("solution.out","w",stdout);
 
     n=read();
     for (int i=;i<=n;i++)
         a[i].s=read(),a[i].m=read(),a[i].r=read();
     m=read();
     for (int i=;i<=m;i++)
     {
         int t=read(),x=read(),y=read();
         hd[x].push_back(t);
         ed[y].push_back(t);
     }
     q.insert(-),q.insert(1e9+);//放一个哨兵。
 
     for (int i=;i<=n;i++)
     {
         for (int j=;j<hd[i].size();j++)
         {
             z1 qq=q.lower_bound(hd[i][j]),hj=q.upper_bound(hd[i][j]);qq--;
             if (*qq==-&&*hj==1e9+) q.insert(hd[i][j]);
             else if (*qq==-)
             {
                 q.insert(hd[i][j]);
                 add(root,,,*hj-hd[i][j],);
             }
             else if (*hj==1e9+)
             {
                 q.insert(hd[i][j]);
                 add(root,,,hd[i][j]-*qq,);
                 //cout<<hd[i][j]-*qq<<"     flag"<<endl;
             }
             else
             {
                 add(root,,,*hj-*qq,-);
                 q.insert(hd[i][j]);
                 add(root,,,hd[i][j]-*qq,),add(root,,,*hj-hd[i][j],);
             }
         }
         int up=ceil(a[i].m*1.0/(double)a[i].r);
         ans+=query1(root,,,,up-)*a[i].r;
         ans+=query2(root,,,up,)*a[i].m;
         z1 t=q.begin();t++;
         if (*t!=)
         {
             if (*t*a[i].r+a[i].s>a[i].m) ans+=a[i].m;
             else ans+=*t*a[i].r+a[i].s;
         }
         for (int j=;j<ed[i].size();j++)
         {
             z1 qq=q.lower_bound(ed[i][j]),hj=q.upper_bound(ed[i][j]);qq--;
             if (*qq==-&&*hj==1e9+) q.erase(ed[i][j]);
             else  if (*qq==-)
             {
                 q.erase(ed[i][j]);
                 add(root,,,*hj-ed[i][j],-);
             }
             else if (*hj==1e9+)
             {
                 q.erase(ed[i][j]);
                 add(root,,,ed[i][j]-*qq,-);
             }
             else
             {
                 add(root,,,ed[i][j]-*qq,-),add(root,,,*hj-ed[i][j],-);
                 q.erase(ed[i][j]);
                 add(root,,,*hj-*qq,);
             }
         }
     //    cout<<ans<<endl;
     }
     printf("%lld",ans);
 }