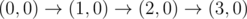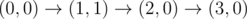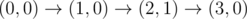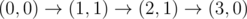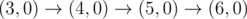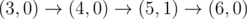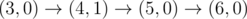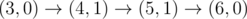Codeforces Round #420 (Div. 2) E. Okabe and El Psy Kongroo DP+矩阵快速幂加速

E. Okabe and El Psy Kongroo

 

 

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).

Additionally, there are n horizontal line segments, the i-th of which goes from x = ai to x = bi inclusive, and is at y = ci. It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ ciwhen his x value satisfies ai ≤ x ≤ bi, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.

Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 109 + 7.

Input

The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of segments and the destination xcoordinate.

The next n lines contain three space-separated integers ai, bi, and ci (0 ≤ ai < bi ≤ 1018, 0 ≤ ci ≤ 15) — the left and right ends of a segment, and its y coordinate.

It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n.

Output

Print the number of walks satisfying the conditions, modulo 1000000007 (109 + 7).

Examples

input

1 3
0 3 3

output

4

 

Note

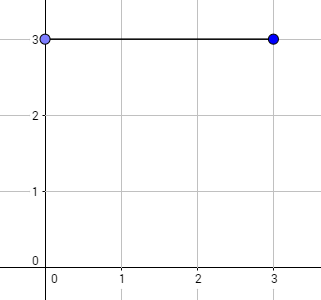
The graph above corresponds to sample 1. The possible walks are:

• 
• 
• 
• 

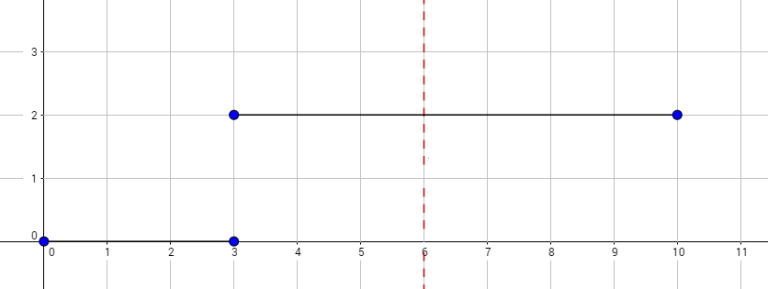
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:

• 
• 
• 
• 

题意：

　　给你一个起点(0,0),和终点(k,0)

　　假设现在在(x,y)，下一步你可以走到(x+1,y)、(x+1,y-1)、(x+1,y+1)；

　　但是不能超过给定的上界线段和正x轴，也就是每一步都要在这两个线段中间

　　问你有多少种走法，走到终点

题解：

　　C很小，只有15

　　每个点向左边走一步，就是， dp[x][y]==》dp[x+1][y]、dp[x+1][y+1]、dp[x+1][y-1]，

　　x最多走10^18步，y最多15，用矩阵快速幂加速求解这个dp方程

#include<bits/stdc++.h>
using namespace std;
#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+1LL;
const double Pi = acos(-1.0);
const int N = 1e4+, M = 1e3+, inf = 2e9;
LL mod =  1e9+;

LL a[N],b[N];
int c[N],n;
struct Matix {
    LL arr[][];
}E,first,dp[];
Matix mul(Matix a,Matix b,LL hang ,LL lie) {
    Matix ans;
    memset(ans.arr,,sizeof(ans.arr));
    for(int i=;i<=hang;i++) {
      for(int t=;t<=lie;t++)
        for(int j=;j<=lie;j++) {
         ans.arr[i][t]+=(a.arr[i][j]*b.arr[j][t])%mod,
         ans.arr[i][t]%=mod;
        }
    }
    return ans;
}

Matix multi (Matix a, Matix b,int hang,int lie,int lie2) {
    Matix ans;
    memset(ans.arr,,sizeof(ans.arr));
    for(int i = ; i < hang; i++) {
        for(int j = ; j < lie2; j++) {
            ans.arr[i][j] = ;
            for(int k = ; k < lie; k++)
                ans.arr[i][j] += (a.arr[i][k] * b.arr[k][j])%mod,
            ans.arr[i][j] %= mod;
        }
    }
    return ans;
}

Matix pow(Matix ans,Matix a,LL x,int cc) {
    while(x) {
        if(x&) ans=multi(ans,a,,cc+,cc+);
        a=mul(a,a,cc,cc);
        x/=;
    }
    return ans;
}
LL K;
int main() {
    scanf("%d%lld",&n,&K);
    for(int i = ; i <= n; ++i) {
        scanf("%lld%lld%d",&a[i],&b[i],&c[i]);
    }
    dp[].arr[][] = ;
    for(int i = ; i <= n; ++i) {
        memset(first.arr,,sizeof(first.arr));
        for(int j = ; j <= c[i]; ++j) first.arr[][j] = dp[i-].arr[][j];
        memset(E.arr,,sizeof(E.arr));
        int sum = ;
        for(int j = ; j <= c[i]; ++j) {
            if(sum) E.arr[][j] = ,sum--;
        }
        int fir = ;
        for(int j = ; j <= c[i]; ++j) {
            for(int k = fir; k <= min(fir+,c[i]); ++k) {
                E.arr[j][k] = ;
            }
            fir++;
        }
        dp[i] = pow(first,E,min(b[i],K) - a[i],c[i]);
      //  dp[i] = multi(first,E,1,c[i]+1,c[i]+1);
    }
    printf("%lld\n",(dp[n].arr[][]+mod)%mod);
    return ;
}