【HDOJ6333】Harvest of Apples（莫队）

题意：

给定T组询问，每组有两个数字n和m，求sigma i=0..m c(n,i) 答案对1e9+7取模

T<=1e5

1<=n,m<=1e5

思路：

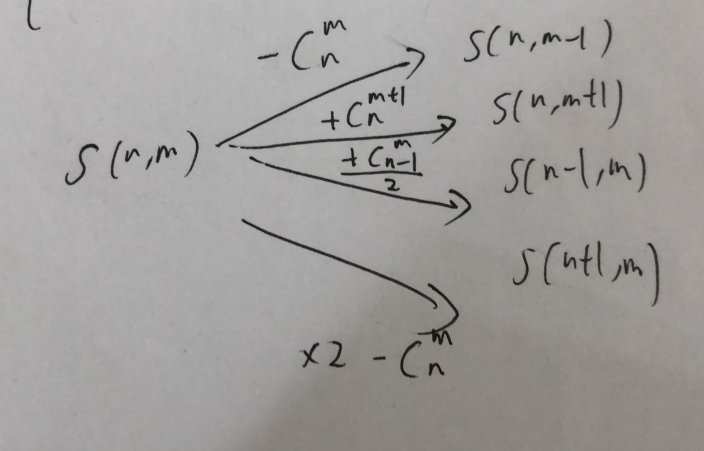
注意要先变n再变m，否则会因n太小有些组合数会丢失

关键点在于n的转移,m的转移谁都会

预处理数组越界要小心

 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef vector<int> VI;
 #define fi first
 #define se second
 #define MP make_pair
 #define MOD 1000000007
 #define N   110000

 struct data{int x,y,id;}a[N];
 ll ans[N+],fac[N+],inv[N+],inv2;
 int pos[N+],m;

 bool cmp(data a,data b)
 {
     if(pos[a.x]==pos[b.x]) return a.y<b.y;
     return a.x<b.x;
 }

 int read()
 {
    int v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }

 ll c(int x,int y)
 {
     ll t=fac[x]*inv[y]%MOD*inv[x-y]%MOD;
     return t;
 }

 void solve()
 {
     ll sum=;
     for(int i=;i<=a[].y;i++) sum=(sum+c(a[].x,i))%MOD;
     int nowx=a[].x,nowy=a[].y;
     ans[a[].id]=sum;
     for(int i=;i<=m;i++)
     {
         while(nowx>a[i].x)
         {
             sum=(sum+c(nowx-,nowy))%MOD;
             sum=sum*inv2%MOD;
             nowx--;
           }
           while(nowx<a[i].x)
         {
             sum=(sum*-c(nowx,nowy)+MOD)%MOD;
             nowx++;
         }
         while(nowy>a[i].y)
         {
             sum=(sum-c(nowx,nowy)+MOD)%MOD;
             nowy--;
         }
         while(nowy<a[i].y)
         {
             sum=(sum+c(nowx,nowy+)+MOD)%MOD;
             nowy++;
         }
         ans[a[i].id]=sum;
     }
 } 

 void init()
 {
     fac[]=;
     for(int i=;i<=N;i++) fac[i]=fac[i-]*i%MOD;
     inv[]=inv[]=;
     for(int i=;i<=N;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
     inv2=inv[];
     for(int i=;i<=N;i++) inv[i]=inv[i-]*inv[i]%MOD;
     int block=int(sqrt(N));
     for(int i=;i<=N;i++) pos[i]=(i-)/block+;
 }

 int main()
 {
       //freopen("1.in","r",stdin);
     //freopen("1.out","w",stdout);
     scanf("%d",&m);
     for(int i=;i<=m;i++)
     {
         scanf("%d%d",&a[i].x,&a[i].y);
         a[i].id=i;
     }
     init();
     sort(a+,a+m+,cmp);
     solve();
     for(int i=;i<=m;i++) printf("%lld\n",ans[i]);
     return ;
 }