优化公式排版和Beamer相关知识

做优化的同学可能会碰到排列形如

max    *******

s.t.   ***** = *

       ***** > ***

       ... 

  的格式

既要要求 max 和 s.t. 对齐  又要令约束式的 = >  等符号对齐！

下面几个代码以供参考：

\begin{align*}

&\max\quad z=\sum\limits_{i=1}^m c_i x_i\\

& \begin{array}{r@{\quad}r@{}l@{\quad}l}

s.t.&\sum\limits_{j=1}^m a_{ij} x_j&\leq b_i,  &i=1,2,3\ldots,n\\

 &x_j&\geq110,  &i=1,2,3\ldots,n  \\

 &x_j&\geq10,  &i=1,2,3\ldots,n  \\

 &x_j&\geq0,  &i=1,2,3\ldots,n  \\

& x_j&\geq0,  &i=1,2,3\ldots,n  \\

\end{array} .

\end{align*}

效果：

\begin{align*}

&\max\,\, z=\sum_{j=1}^n c_jx_j\\

&s.t.\quad

\begin{cases}

\sum\limits_{j=1}^n a_{ij}x_j \leq b_i & (i=1,2,3,\cdots, m), \\

x_j \geq 0 & (j=1,2,3,\cdots,n).

\end{cases}

\end{align*}

 

 

\begin{equation*}

\begin{split}

&\max \,\, z=\sum_{j=1}^nc_jx_j\\

&s.t.\quad  \left\{\begin{array}{lc}

\sum_{j=1}^na_{ij}x_j\leq b_j,\quad & (i=1,2,\cdots,m)\\

x_j\geq 0,\quad & (j=1,2,\cdots,n) \end{array}\right.

\end{split}

\end{equation*}

 

\begin{align*}

&\max\,\,z=\sum\limits_{j=1}^nc_jx_j\\

&s.t.\begin{cases}\sum_{j=1}^na_{ij}x_j\leq b_i&(i=1,2,\cdots,m)\\

x_j\geq0&(j=1,2,\cdots,n)\end{cases}\\

\end{align*}

 

 

from: http://blog.sina.com.cn/s/blog_6850cf720101a9kk.html

 

默认一个frame就是一页slide，要想一个frame显示在多个silde里可以设置分页
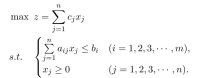
\begin{frame}[allowframebreaks=1]{this frame name}

\begin{theorem}[some therorem]
$a^{2}=...$ hahha 
\end{theorem}

\begin{Definition}[new definition]
a is a ...
\end{Definition}

自定义类似公式的block
\begin{block}{some therorem}
$a^{2}=...$ hahha 
\end{block}

自定义类似block的文本框
\setbeamercolor{bgcolor}{fg=black,bg=blue!20}

\begin{beamercolorbox}[rounded=true, shadow=true,wd=12cm]{bgcolor}
   $a^{2}=...$ hahha 
\end{beamercolorbox}

 

公式希腊字符的加粗
\usepackage{bm}
 $\bm

数学中的实数域 那种符号的字体

\usepackage{dsfont}
$x in \mathds{R} $

算法

\usepackage{algorithm} %format of the algorithm
\usepackage{algorithmic}

\begin{algorithm}[H]
  \caption{ABC($A$)}
 \scriptsize  %下面的字特小号
  \begin{algorithmic}[]
    \STATE initialization $U^{(n)}$
    \REPEAT
        \FOR{n=,..,N}
          \STATE $ C  \leftarrow B $
        \ENDFOR
       \IF{xtrue}
          \STATE $ x $
        \ENDIF
    \UNTIL{ convergence}

    \STATE \STATE $ C  \leftarrow B $
  \end{algorithmic}
\end{algorithm}

其它让算法表小或分页的方法--待测试
\captionof{algorithm}{xxx}
 \scalebox{0.9}{
\SetAlFnt{\footnotesize}

---

Beamer中block的样式（三种:normal, alert和example，这三种分别是蓝,红和绿色），也可以进行修改

\documentclass{beamer}
\usetheme{Warsaw}
\begin{document}
\title{title}
\author{Frogge}
\institute{XX}
\date{\today}
\begin{frame}
  \titlepage
\end{frame}

\begin{frame}\frametitle{Three default block styles}
\begin{block}{Block}
This is a block
\end{block}

\begin{alertblock}{Alert block}
This is an alert block.
\end{alertblock}

\begin{exampleblock}{Example block}
This is an example block.
\end{exampleblock}
\end{frame}

\begin{frame}\frametitle{User-defined blcok styles}

\setbeamercolor{uppercol}{fg=white,bg=green!!black}%
\setbeamercolor{lowercol}{fg=black,bg=green!}%
\begin{beamerboxesrounded}[upper=uppercol,lower=lowercol,shadow=true]{Something}
This is a user-defined blcok.
\end{beamerboxesrounded}

\end{frame}

\begin{frame}\frametitle{Columns}
\begin{columns}
  \begin{column}{0.48\textwidth}
    \begin{alertblock}{Alert block}
      This is an alert block.
    \end{alertblock}
  \end{column}

  \begin{column}{0.48\textwidth}
    \begin{exampleblock}{Example block}
      This is an example block.
    \end{exampleblock}
  \end{column}
\end{columns}
\end{frame}

\end{document}