「BZOJ4510」「Usaco2016 Jan」Radio Contact 解题报告

无线电联系 Radio Contact

题目描述

Farmer John has lost his favorite cow bell, and Bessie the cow has agreed to help him find it! They both fan out and search the farm along different paths, but stay in contact via radio so they can keep in touch with each-other. Unfortunately, the batteries in their radios are running low, so they want to plan their movements so as to conserve power, by trying to stay always within a short distance apart.

Farmer John starts at location (\(f_x, f_y\)) and plans to follow a path consisting of NN steps, each of which is either 'N' (north), 'E' (east), 'S' (south), or 'W' west. Bessie starts at location (\(b_x, b_y\)) and follows a similar path consisting of MM steps. Both paths may share points in common. At each time step, Farmer John can either stay put at his current location, or take one step forward along his path, in whichever direction happens to be next (assuming he has not yet reached the final location in his path). Bessie can make a similar choice. At each time step (excluding the first step where they start at their initial locations), their radios consume energy equal to the square of the distance between them.

Please help FJ and Bessie plan a joint movement strategy that will minimize the total amount of energy consumed up to and including the final step where both of them first reach the final locations on their respective paths.

FJ失去了他最喜欢的牛铃，而Bessie已经同意帮助他找到它！他们用不同的路径搜索农场，通过无线电保持联系。不幸的是，无线电中的电池电量不足，所以他们设法尽可能保持两者位置的距离最小，以节省电量。

FJ从位置\((f_x,f_y)\)开始，并计划遵循由N步骤组成的路径，每个步骤都是“N”（北），“E”（东），“S”（南），或“W”（西）。Bessie从位置\((b_x,b_y)\)开始，并遵循由M步骤组成的类似路径。两个路径可以经过相同的点。在每个时间段，FJ可以保持在他现在的位置，或沿着他的道路前进一步，无论哪个方向恰好在下一个（假设他还没有到达他的路径的最后位置）。Bessie可以做出类似的选择。在每个时间步（不包括从初始位置开始的第一步），他们的无线电消耗的能量等于它们之间距离的平方。

请帮助FJ和Bessie计划行动策略，最大限度地减少消耗的能量总量。总量包括最终步骤，这时两者首先到达各自路径上的最终位置。

输入输出格式

输入格式：

The first line of input contains \(N\) and \(M\) (\(1 \le N, M \le 1000\)). The second line contains integers \(f_x\) and \(f_y\), and the third line contains \(b_x\) and \(b_y\) (\(0 \le f_x, f_y, b_x, b_y \le 1000\)). The next line contains a string of length \(N\) describing FJ's path, and the final line contains a string of length \(M\) describing Bessie's path. It is guranteed that Farmer John and Bessie's coordinates are always in the range (\(0 \le x,y \le 1000\)) throughout their journey. Note that East points in the positive x direction and North points in the positive y direction.

第一行输入\(N\)和\(M\)（\(1 \le N,M \le 1000\)）。

第二行输入整数\(f_x\)和\(f_y\)，第三行输入\(b_x\)和\(b_y\)\((0 \le f_x,f_y,b_x,b_y \le 1000)\)。下一行包含一个长度为N的字符串描述FJ的路径，最后一行包含一个字符串的长度\(M\)描述Bessie的路径。

数据满足\((0 \le x,y \le 1000)\)。注意，东方向为正X方向，北方向为正Y方向。

输出格式：

Output a single integer specifying the minimum energy FJ and Bessie can use

during their travels.

输出一个整数，表示最小能量。

输入输出样例

输入样例#1：

2 7
3 0
5 0
NN
NWWWWWN

输出样例#1：

28

---

思路

众所周知，DP是一个好东西，所以这题用DP。

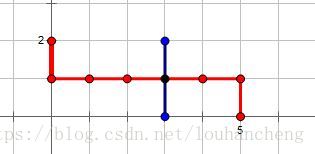
这是样例的示意图

这道题有十分明显的阶段性，而且数据也不大，所以用DP即可。

我们用一个二维数组f[i][j]表示当Farmer John到第i步，Bessie到第j步时所需花费的最小能量。

转移方程容易推得：

f[i][j] = min( f[i][j - 1], f[i - 1][j], f[i - 1][j - 1] ) + dist;

其中dist表示FJ在第i步，Bessie在j步时他们距离的平方\(( tx1 - tx2 ) \times ( tx1 - tx2 ) + ( ty1 - ty2 ) \times ( ty1 - ty2 )\)

这里要注意初始化:

f[i][0] = f[i - 1][0] + dist;
f[0][i] = f[i - 1][0] + dist;
f[0][0] = 0;//因为从初始位置开始的第一步不需要能量

这里我用一个move函数移动坐标(用了引用变量方便一点)

代码

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
#define MAXN 1005
#define LL long long

int N, M;
LL f[MAXN][MAXN];//开long long防止上溢
int fx, fy, bx, by, la, lb;
char a[MAXN], b[MAXN];//移动方向

void move( int &x, int &y, char d ){ //移动坐标
    switch( d ){
        case 'N': y++; break;
        case 'S': y--; break;
        case 'W': x--; break;
        case 'E': x++; break;
    }
}

LL dist( int x1, int y1, int x2, int y2 ){ //花费能量
    return ( x1 - x2 ) * ( x1 - x2 ) + ( y1 - y2 ) * ( y1 - y2 );
}

int main(){
    scanf( "%d%d", &N, &M );
    scanf( "%d%d%d%d", &fx, &fy, &bx, &by );
    scanf( "%s%s", a + 1, b + 1 );
    la = strlen( a + 1 ); lb = strlen( b + 1 );
    int tx1(fx), ty1(fy), tx2(bx), ty2(by);//FJ、Bessie的坐标
    for ( int i = 1; i <= la; ++i ){ // 初始化f[i][0](i != 0)
        move( tx1, ty1, a[i] );
        f[i][0] = f[i - 1][0] + dist( tx1, ty1, bx, by );
    }
    for ( int i = 1; i <= lb; ++i ){ //初始化f[0][i](i != 0)
        move( tx2, ty2, b[i] );
        f[0][i] = f[0][i - 1] + dist( fx, fy, tx2, ty2 );
    }
    tx1 = fx; ty1 = fy;
    for ( int i = 1; i <= la; ++i ){
        tx2 = bx; ty2 = by;
        move( tx1, ty1, a[i] );
        for ( int j = 1; j <= lb; ++j ){
            move( tx2, ty2, b[j] );
            f[i][j] = min( f[i - 1][j], f[i][j - 1] ); // 上述转移方程
            f[i][j] = min( f[i][j], f[i - 1][j - 1] );
            f[i][j] += dist( tx1, ty1, tx2, ty2 );
        }
    }
    printf( "%lld", f[la][lb] );
    return 0;
}

** 所以: DP是个好东西 **