Math: Fibonacci
https://www.zhihu.com/question/28062458
http://blog.csdn.net/hikean/article/details/9749391
对于Fibonacci数列,1,1,2,3,5,8,13,21...
long fib(int n)
{
if (n == || n == )
{
return ;
}
return fib(n-) + fib(n-);
}
long fib(int n)
{
if (n == || n == )
{
return ;
}
vector <long> fibs(, );
for (int i = ; i <= n; ++i)
{
fibs.push_back(fibs[i-] + fibs[i-]);
}
return fibs[n];
}
long fib(int n)
{
if (n == || n == )
{
return ;
} int fib[];
fib[] = fib[] = ;
int idx = ;
for (int i = ; i <= n; ++i)
{
idx = (idx + ) % ;
fib[idx] = fib[(idx + )%] + fib[(idx + )%];
}
return fib[idx];
}

所以,

现在问题是如何快速计算一个矩阵的n次方。这里可以利用A^n = A^(n/2)*A^(n/2) * (n % 2 == 1 ? A : I)进行分治。
matrix power(matrix A, int n)
{
matrix ans = I;
while(n > )
{
if (n % == )
{
ans *= A;
}
A *= A;
n /= ;
}
return ans;
}
这个算法的时间复杂度是O(logN).
对于矩阵的 n 次方求解,可以通过矩阵的特征值分解来完成。过程如下:

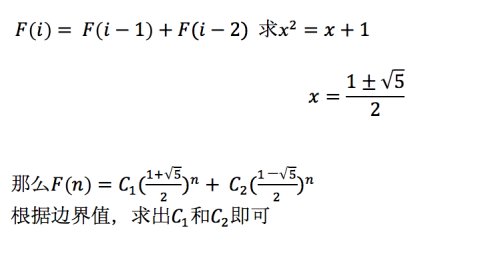
Math: Fibonacci的更多相关文章
- 从零开始学习Node.js例子四 多页面实现数学运算
app-node.js ; var http = require('http'); var htutil = require('./htutil'); var server = http.create ...
- JUnit4单元测试入门教程
本文按以下顺序讲解JUnit4的使用 下载jar包 单元测试初体验 自动生成测试类 执行顺序 @Test的属性 下载jar包## 下载地址 在github上,把以下两个jar包都下载下来. 下 ...
- 山东省第七届ACM省赛------Fibonacci
Fibonacci Time Limit: 2000MS Memory limit: 131072K 题目描述 Fibonacci numbers are well-known as follow: ...
- Applying Eigenvalues to the Fibonacci Problem
http://scottsievert.github.io/blog/2015/01/31/the-mysterious-eigenvalue/ The Fibonacci problem is a ...
- wikioi 1973 Fibonacci数列【输出第N项的值】
/*===================================== 1978 Fibonacci数列 3 题目描述 Description 斐波纳契数列是这样的数列: f1 = 1 f2 ...
- Project Euler 104:Pandigital Fibonacci ends 两端为全数字的斐波那契数
Pandigital Fibonacci ends The Fibonacci sequence is defined by the recurrence relation: F[n] = F[n-1 ...
- 斐波那契(Fibonacci)数列的七种实现方法
废话不多说,直接上代码 #include "stdio.h" #include "queue" #include "math.h" usin ...
- 蓝桥杯 入门训练 Fibonacci数列
入门训练 Fibonacci数列 时间限制:1.0s 内存限制:256.0MB 问题描述 Fibonacci数列的递推公式为:Fn=Fn-1+Fn-2,其中F1=F2=1. ...
- 第2章 数字之魅——斐波那契(Fibonacci)数列
斐波那契(Fibonacci)数列 问题描述 递归算法: package chapter2shuzizhimei.fibonacci; /** * Fibonacci数列递归求解 * @author ...
随机推荐
- [JZOJ 5817] 抄代码
题意: 给定2T个串,带修的判断两个串是否按规则一样?? 思路: 两个串是"抄袭的"肯定就是: 1.长度一样. 2.特殊字符位置一样 3.对于每个\(x\)在两个串中出现位置一样, ...
- iOS 获取音频或是视频的时间
AVURLAsset* audioAsset =[AVURLAssetURLAssetWithURL:audioFileURL options:nil]; CMTime audioDuration = ...
- sqlalchemy session
Cookie cookie是浏览器保存在用户电脑上的一小段文本,用来保存用户在网站上的必要的信息.Web页面或服务器告诉浏览器按照一定的规范存储这些信息,并且在以后的所有请求中,这些信息就会自动加在h ...
- windows中创建流量转发规则
#创建流量转发,其中listenaddress为内网ip(也就是ipconfig中所显示的IP),listenport为监听的本机对外端口,后两个分别是需转发的目标主机IP和端口. netsh int ...
- debian 源设置 ( apt-get 不能安装)
使用说明 以Jessie为例, 编辑/etc/apt/sources.list文件, 在文件最前面添加以下条目(操作前请做好相应备份) deb http://mirrors.163.com/debia ...
- 剑指offer——33分行从上到下打印二叉树
题目描述 从上到下按层打印二叉树,同一层结点从左至右输出.每一层输出一行. 题解: 使用BFS,按层打印即可 class Solution { public: vector<vector&l ...
- Shiro术语
请花2分钟阅读和理解Shiro中的术语 - 这是非常重要的.这里的术语和概念在文档中的任何地方都被引用,并且将大大简化您对Shiro和一般的安全性的理解. 因为使用了一些您可能不太明白的术语,所以安全 ...
- nodejs中命令行和node交互模式的区分
来自:廖雪峰教程 么么哒~ 命令行模式和Node交互模式 请注意区分命令行模式和Node交互模式. 看到类似C:\>是在Windows提供的命令行模式: 在命令行模式下,可以执行node进入No ...
- [转载]Spring AOP 深入剖析
转载自 http://www.cnblogs.com/digdeep/p/4528353.html 多谢@digdeep AOP是Spring提供的关键特性之一.AOP即面向切面编程,是OOP编程的有 ...
- 03->OpenGL多边形,glut实现三角形条带和三角形扇
图形学中基本图元是多边形,一般要求是凸多边形,三角形是最简单的凸多边形,在图形渲染中比一般多边形其绘制速度快.今天学习OpenGL绘制三角形条带和三角形扇基础.编程环境! 1. 三角形条带 指定顶点序 ...
