Intersection（Check）

Intersection

http://poj.org/problem?id=1410

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 17591		Accepted: 4516

Description

You are to write a program that has to decide whether a given line segment intersects a given rectangle.

An example: 
line: start point: (4,9) 
end point: (11,2) 
rectangle: left-top: (1,5) 
right-bottom: (7,1)

 
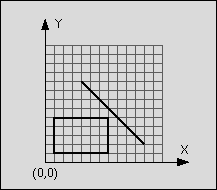
Figure 1: Line segment does not intersect rectangle

The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.

Input

The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format: 
xstart ystart xend yend xleft ytop xright ybottom

where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.

Output

For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.

Sample Input

1
4 9 11 2 1 5 7 1

Sample Output

F

判断线是否在矩形内或与矩形的边相交

注意共线但是不相交的情况

Check为判断线段是否相交

 #include<cstdio>
 #include<iostream>
 #include<cstring>
 #include<cmath>
 using namespace std;
 const double eps=1e-;
 const double INF=1e20;
 const double PI=acos(-1.0);
 const int maxp=;
 int sgn(double x){
     if(fabs(x)<eps) return ;
     if(x<) return -;
     else return ;
 }
 inline double sqr(double x){return x*x;}
 struct Point{
     double x,y;
     Point(){}
     Point(double _x,double _y){
         x=_x;
         y=_y;
     }
     void input(){
         scanf("%lf %lf",&x,&y);
     }
     void output(){
         printf("%.2f %.2f\n",x,y);
     }
     bool operator == (const Point &b)const{
         return sgn(x-b.x) ==  && sgn(y-b.y)== ;
     }
     bool operator < (const Point &b)const{
         return sgn(x-b.x)==?sgn(y-b.y)<:x<b.x;
     }
     Point operator - (const Point &b)const{
         return Point(x-b.x,y-b.y);
     }
     //叉积
     double operator ^ (const Point &b)const{
         return x*b.y-y*b.x;
     }
     //点积
     double operator * (const Point &b)const{
         return x*b.x+y*b.y;
     }
     //返回长度
     double len(){
         return hypot(x,y);
     }
     //返回长度的平方
     double len2(){
         return x*x+y*y;
     }
     //返回两点的距离
     double distance(Point p){
         return hypot(x-p.x,y-p.y);
     }
     Point operator + (const Point &b)const{
         return Point(x+b.x,y+b.y);
     }
     Point operator * (const double &k)const{
         return Point(x*k,y*k);
     }
     Point operator / (const double &k)const{
         return Point(x/k,y/k);
     }

     //计算pa和pb的夹角
     //就是求这个点看a,b所成的夹角
     ///LightOJ1202
     double rad(Point a,Point b){
         Point p=*this;
         return fabs(atan2(fabs((a-p)^(b-p)),(a-p)*(b-p)));
     }
     //化为长度为r的向量
     Point trunc(double r){
         double l=len();
         if(!sgn(l)) return *this;
         r/=l;
         return Point(x*r,y*r);
     }
     //逆时针转90度
     Point rotleft(){
         return Point(-y,x);
     }
     //顺时针转90度
     Point rotright(){
         return Point(y,-x);
     }
     //绕着p点逆时针旋转angle
     Point rotate(Point p,double angle){
         Point v=(*this) -p;
         double c=cos(angle),s=sin(angle);
         return Point(p.x+v.x*c-v.y*s,p.y+v.x*s+v.y*c);
     }
 };

 struct Line{
     Point s,e;
     Line(){}
     Line(Point _s,Point _e){
         s=_s;
         e=_e;
     }
     bool operator==(Line v){
         return (s==v.s)&&(e==v.e);
     }
     //根据一个点和倾斜角angle确定直线，0<=angle<pi
     Line(Point p,double angle){
         s=p;
         if(sgn(angle-PI/)==){
             e=(s+Point(,));
         }
         else{
             e=(s+Point(,tan(angle)));
         }
     }
     //ax+by+c=0;
     Line(double a,double b,double c){
         if(sgn(a)==){
             s=Point(,-c/b);
             e=Point(,-c/b);
         }
         else if(sgn(b)==){
             s=Point(-c/a,);
             e=Point(-c/a,);
         }
         else{
             s=Point(,-c/b);
             e=Point(,(-c-a)/b);
         }
     }
     void input(){
         s.input();
         e.input();
     }
     void adjust(){
         if(e<s) swap(s,e);
     }
     //求线段长度
     double length(){
         return s.distance(e);
     }
     //返回直线倾斜角 0<=angle<pi
     double angle(){
         double k=atan2(e.y-s.y,e.x-s.x);
         if(sgn(k)<) k+=PI;
         if(sgn(k-PI)==) k-=PI;
         return k;
     }
     //点和直线的关系
     //1 在左侧
     //2 在右侧
     //3 在直线上
     int relation(Point p){
         int c=sgn((p-s)^(e-s));
         if(c<) return ;
         else if(c>) return ;
         else return ;
     }
     //点在线段上的判断
     bool pointonseg(Point p){
         return sgn((p-s)^(e-s))==&&sgn((p-s)*(p-e))<=;
     }
     //两向量平行(对应直线平行或重合)
     bool parallel(Line v){
         return sgn((e-s)^(v.e-v.s))==;
     }
     //两线段相交判断
     //2 规范相交
     //1 非规范相交
     //0 不相交
     int segcrossseg(Line v){
         int d1=sgn((e-s)^(v.s-s));
         int d2=sgn((e-s)^(v.e-s));
         int d3=sgn((v.e-v.s)^(s-v.s));
         int d4=sgn((v.e-v.s)^(e-v.s));
         if((d1^d2)==-&&(d3^d4)==-) return ;
         return (d1==&&sgn((v.s-s)*(v.s-e))<=||
                 d2==&&sgn((v.e-s)*(v.e-e))<=||
                 d3==&&sgn((s-v.s)*(s-v.e))<=||
                 d4==&&sgn((e-v.s)*(e-v.e))<=);
     }
     //直线和线段相交判断
     //-*this line -v seg
     //2 规范相交
     //1 非规范相交
     //0 不相交
     int linecrossseg(Line v){
         int d1=sgn((e-s)^(v.s-s));
         int d2=sgn((e-s)^(v.e-s));
         if((d1^d2)==-) return ;
         return (d1==||d2==);
     }
     //两直线关系
     //0 平行
     //1 重合
     //2 相交
     int linecrossline(Line v){
         if((*this).parallel(v))
             return v.relation(s)==;
         return ;
     }
     //求两直线的交点
     //要保证两直线不平行或重合
     Point crosspoint(Line v){
         double a1=(v.e-v.s)^(s-v.s);
         double a2=(v.e-v.s)^(e-v.s);
         return Point((s.x*a2-e.x*a1)/(a2-a1),(s.y*a2-e.y*a1)/(a2-a1));
     }
     //点到直线的距离
     double dispointtoline(Point p){
         return fabs((p-s)^(e-s))/length();
     }
     //点到线段的距离
     double dispointtoseg(Point p){
         if(sgn((p-s)*(e-s))<||sgn((p-e)*(s-e))<)
             return min(p.distance(s),p.distance(e));
         return dispointtoline(p);
     }
     //返回线段到线段的距离
     //前提是两线段不相交，相交距离就是0了
     double dissegtoseg(Line v){
         return min(min(dispointtoseg(v.s),dispointtoseg(v.e)),min(v.dispointtoseg(s),v.dispointtoseg(e)));
     }
     //返回点P在直线上的投影
     Point lineprog(Point p){
         return s+(((e-s)*((e-s)*(p-s)))/((e-s).len2()));
     }
     //返回点P关于直线的对称点
     Point symmetrypoint(Point p){
         Point q=lineprog(p);
         return Point(*q.x-p.x,*q.y-p.y);
     }
 };

 Line L[];
 int book[];
 int n;

 bool Check(Line a,Line b){
     if(sgn((a.s-a.e)^(b.s-a.e))*sgn((a.s-a.e)^(b.e-a.e))>) return false;
     if(sgn((b.s-b.e)^(a.s-b.e))*sgn((b.s-b.e)^(a.e-b.e))>) return false;
     if(sgn(max(a.s.x,a.e.x)-min(b.s.x,b.e.x))>=&&sgn(max(b.s.x,b.e.x)-min(a.s.x,a.e.x))>=
      &&sgn(max(a.s.y,a.e.y)-min(b.s.y,b.e.y))>=&&sgn(max(b.s.y,b.e.y)-min(a.s.y,a.e.y))>=)
         return true;
     else return false;
 }

 int main(){
     int T;
     scanf("%d",&T);
     while(T--){
         Line seg,L[];
         double x1,y1,x2,y2,x11,y11,x22,y22;
         scanf("%lf %lf %lf %lf",&seg.s.x,&seg.s.y,&seg.e.x,&seg.e.y);
         scanf("%lf %lf %lf %lf",&x11,&y11,&x22,&y22);
         x1=min(x11,x22);
         x2=max(x11,x22);
         y1=min(y11,y22);
         y2=max(y11,y22);
         //上下左右
         L[].s.x=x1,L[].s.y=y1,L[].e.x=x2,L[].e.y=y1;
         L[].s.x=x2,L[].s.y=y2,L[].e.x=x1,L[].e.y=y2;
         L[].s.x=x1,L[].s.y=y2,L[].e.x=x1,L[].e.y=y1;
         L[].s.x=x2,L[].s.y=y1,L[].e.x=x2,L[].e.y=y2;
         int flag=;
         for(int i=;i<=;i++){
             if(Check(seg,L[i])){
                 flag=;
             }
         }
         if(max(seg.s.x,seg.e.x)<=x2&&max(seg.s.y,seg.e.y)<=y2&&min(seg.s.x,seg.e.x)>=x1&&min(seg.s.y,seg.e.y)>=y1){
             flag=;
         }
         if(flag) puts("T");
         else puts("F");
     }
     return ;
 }