希尔排序之python

希尔排序( Shell sort）

插入排序的改进版本，其核心思想是将原数据集合分割成若干个子序列，然后再对子序列分别进行直接插入排序，使子序列基本有序，最后再对全体记录进行一次直接插入排序。

我的面向人类的理解：挑选间隔为k的数进行排序，然后不断缩小k，最终降到1，此时相当于插入排序。

1.算法描述：

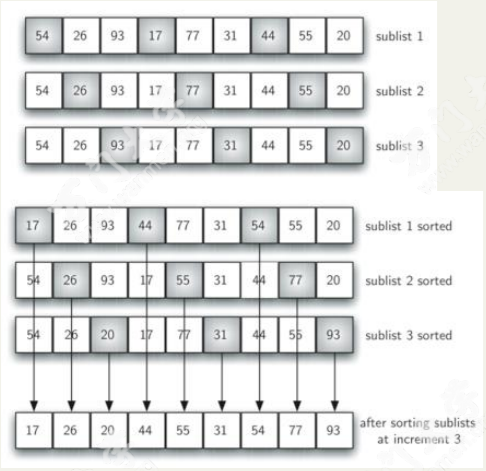
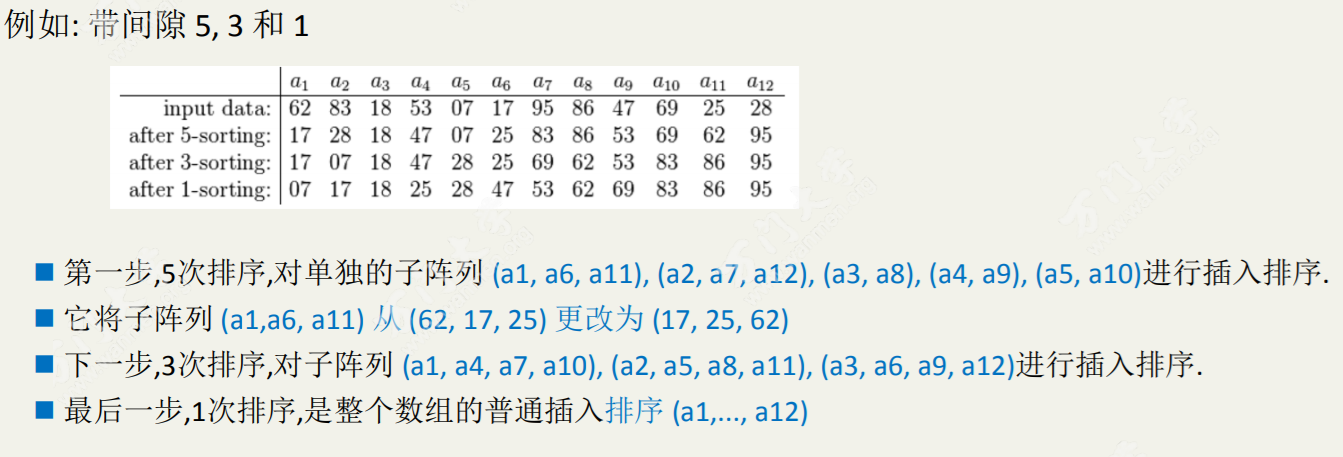
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
2. 按增量序列个数k，对序列进行k 趟排序；
3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

2.算法属性:

• 希尔排序的运行时间很大程度上取决于它使用的间隙顺序
• 对于许多实际的变量，确定它们的时间复杂度仍然是一个公开的问题，大概来说它的运行时间是比O(n^2)要好点的
• 时间复杂度大概：O(n)
• 空间复杂度：O(n√n)
• 稳定性：不稳定

3.代码实现

#相比插入排序，shell排序更适合用于处理data更大的数组

import time
def shell_sort(nums):
    start = time.time()
 
    gap = len(nums)       #先指定len长度给gap后续对gap进行分组子序列
    length = len(nums)
 
    #while用于处理每个大轮的sort
    while (gap > 0):
 
        #两个for循环与插入排序同理
        for i in range(gap, length):
            for j in range(i, gap - 1, -gap):
                if (nums[j - gap] > nums[j]):
                    nums[j], nums[j - gap] = nums[j - gap], nums[j]
 
        if (gap == 2):
            gap = 1
        else:
            gap = gap // 2    #每一次比上一次大概扩大两倍的分组子序列
 
    t = time.time() - start
    return nums, t           
 
lis = [1,2,5,8,4,3,6]
shell_sort(lis)
 
#输出结果
([1, 2, 3, 4, 5, 6, 8], 0.0)