leetcode-全排列详解（回溯算法）

 全排列

 

 

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

参考博客：https://blog.csdn.net/summerxiachen/article/details/60579623

思路： 举例 1 2 3 4

1.回想自己大脑里面对1234的全排列的情况。首先固定1，然后对2 3 4进行分类，也就是固定第二个数字，2  。再往下，就是{1，2} 对3 4进行选择。固定3，排列为 1，2，3，4

固定4，排列为1，2，4，3。

因此我们可以回想到我们对全排列的思路是： 先固定第一个数，剩下的数字进行全排列。比如1，2，3，4固定1之后，就是对2，3，4进行全排列。固定2之后，就是对3，4全排列。

对

T=【T=【x1,x1,x2,x3,x4,x5,........xn−1,xn】x2,x3,x4,x5,........xn−1,xn】

我们获得了在第一个位置上的所有情况之后(注：是所有的情况)，对每一种情况，抽去序列TT中的第一个位置，那么对于剩下的序列可以看成是一个全新的序列

T1=【x2,x3,x4,x5,........xn−1,xn】T1=【x2,x3,x4,x5,........xn−1,xn】

序列T1T1可以认为是与之前的序列毫无关联了。同样的，我们可以对这个T1T1进行与TT相同的操作，直到TT中只一个元素为止。这样我们就获得了所有的可能性。所以很显然，这是一个递归算法。

第一位的所有情况：无非是将x1x1与后面的所有数x2,x3,.......xnx2,x3,.......xn依次都交换一次

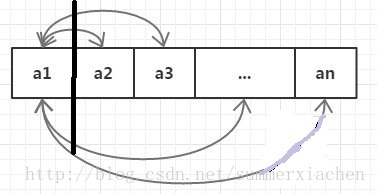
算法思路：全排列可以看做固定前i位，对第i+1位之后的再进行全排列，比如固定第一位，后面跟着n-1位的全排列。那么解决n-1位元素的全排列就能解决n位元素的全排列了，这样的设计很容易就能用递归实现。

代码如下：

class Solution {
    List<List<Integer>> list=new ArrayList();　　　　　　
    public List<List<Integer>> permute(int[] nums) {

       if(nums.length==0)return list;
        backTrace(0,nums.length,nums);
        return list;
    }
    public void backTrace(int i,int len,int [] nums){
        if(i==len-1){               //回溯的返回条件
            List<Integer> res=new ArrayList();
            for(int j=0;j<len;j++){             //回溯到了最后一个数字，我们便可以输出数组
                res.add(nums[j]);
            }
            list.add(res);
            return ;
        }
        for(int j=i;j<len;j++){
            swap(nums,i,j);                     //交换元素，全排列的思想
            backTrace(i+1,len,nums);            //继续回溯，改变i的值，使其向下探索
            swap(nums,i,j);                     //探索找到一个排列后，需要向上回溯，因此要恢复原序列的排列
        }

    }
    public void swap(int[] nums,int i,int j){
        int temp=nums[i];
        nums[i]=nums[j];
        nums[j]=temp;
    }
}

存在相同元素的情况

上面的程序乍一看没有任何问题了。可是，如果我们对序列进行一下修改 array = {1, 2, 2}.我们看看运行的结果会怎么样。

[1, 2, 2]
[1, 2, 2]
[2, 1, 2]
[2, 2, 1]
[2, 2, 1]
[2, 1, 2]

这里出现了好多的重复。重复的原因当然是因为我们列举了所有位置上的可能性，而没有太多地关注其真实的数值。 
现在，我们这样来思考一下，如果有一个序列T = {a1, a2, a3, …, ai, … , aj, … , an}。其中，a[i] = a[j]。那么是不是就可以说，在a[i]上，只要进行一次交换就可以了，a[j]可以直接忽略不计了。好了，基于这样一个思路，我们对程序进行一些改进。我们每一次交换递归之前对元素进行检查，如果这个元素在后面还存在数值相同的元素，那么我们就可以跳过进行下一次循环递归（当然你也可以反着来检查某个元素之前是不是相同的元素）。 
基于这个思路，不难写出改进的代码。如下：

class Solution {
    List<List<Integer>> res=new ArrayList();
    public List<List<Integer>> permute(int[] nums) {
        dfs(nums,0);
        return res;
    }
    public boolean isSame(int[] nums,int start,int end){
        for(int i=start;i<end;i++){
            if(nums[i]==nums[end])return false;
        }
        return true;
    }
    public void dfs(int[] nums,int len){
        if(len==nums.length-1){
            List<Integer> list=new ArrayList();
            for(int i=0;i<nums.length;i++){
                list.add(nums[i]);
            }
            res.add(list);
        }
        for(int i=len;i<nums.length;i++){
            if(!isSame(nums,len,i))continue;
            swap(nums,i,len);
            dfs(nums,len+1);
            swap(nums,len,i);

        }
    }
    public void swap(int[] nums,int i,int j){
        int temp=nums[i];
        nums[i]=nums[j];
        nums[j]=temp;
    }
}