直方图均衡基本原理及Python实现

1. 基本原理

通过一个变换，将输入图像的灰度级转换为`均匀分布`，变换后的灰度级的概率密度函数为

$$P_s(s) = \frac{1}{L-1}$$

直方图均衡的变换为

$$s = T(r) = (L-1)\int_0^r {P_r(c)} \,{\rm d}c $$

• $s$为变换后的灰度级，$r$为变换前的灰度级
• $P_r(r)$为变换前的概率密度函数

2. 测试结果

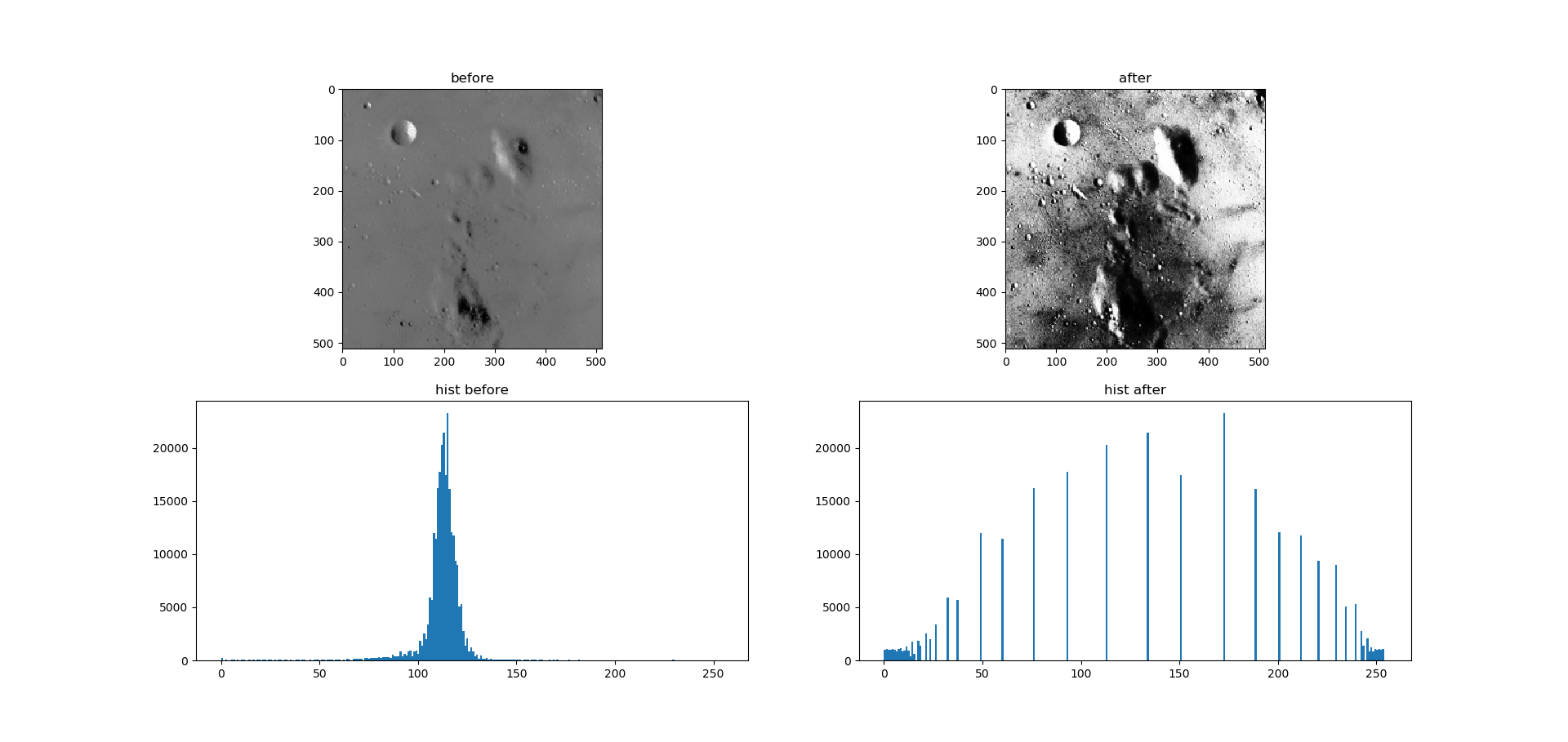
图源自skimage

3.代码

 import numpy as np

 def hist_equalization(input_image):
     '''
     直方图均衡（适用于灰度图）
     :param input_image: 原图像
     :return: 均衡后的图像
     '''
     output_imgae = np.copy(input_image) # 输出图像，初始化为输入

     input_image_cp = np.copy(input_image) # 输入图像的副本

     m, n = input_image_cp.shape # 输入图像的尺寸（行、列）

     pixels_total_num = m * n # 输入图像的像素点总数

     input_image_grayscale_P = [] # 输入图像中各灰度级出现的概率，亦即输入图像直方图

     # 求输入图像中各灰度级出现的概率，亦即输入图像直方图
     for i in range(256):
         input_image_grayscale_P.append(np.sum(input_image_cp == i) / pixels_total_num)

     # 求解输出图像
     t = 0               # 输入图像的灰度级分布函数F
     for i in range(256):

         t = t + input_image_grayscale_P[i]

         output_imgae[np.where(input_image_cp == i)] = 255 * t

     return output_imgae

4. 数学证明

目标变换

$$S = T(r)  = (L-1)\int_0^rp_r(w)dw$$

• $T(r)$为严格单调函数，可保证反映射时，消除二义性
• $p_r(w)$为源图像归一化后的直方图

4.1 假定

• 图像灰度级为：$[0, L-1]$
• 源图像中，$k$灰度级的像素个数：$n_k$
• 源图像像素总数：$n$
• 原图像直方图$h(r_k) = n$

4.2 归一化后的直方图

$$p(r_k) = n_k / n$$
$p(r_k)$即为灰度级$r_k$在源图像中出现的概率估计

4.3 证明

概率密度函数的积分为分布函数，即对分布函数的导数为概率密度函数。

因为$p_r(r)$与$T(r)$已知，则由
$$\frac{{\rm d}r}{{\rm d}S} = \frac{p_s(s)}{p_r(r)}$$
又因为
$$S = T(r)$$
即
$$\frac{{\rm d}S}{{\rm d}r}  =  \frac{T(r)}{r}$$
联立上三式及目标变换
$$S = T(r)  = (L-1)\int_0^rp_r(w)dw$$
可得
$$p_s(s) = \frac{1}{L-1}$$
故，这意味着变换之后的图像的灰度级为均匀分布，证毕。