根节点

非叶子节点(决策点)

叶子节点(决策结果)

分支



熵代表混乱程度


信息增益




构造树的基本想法是随着树深度的增加、节点的熵迅速地降低。熵降低的速度越快越好，这样我们有望得到一颗高度最矮的决策树












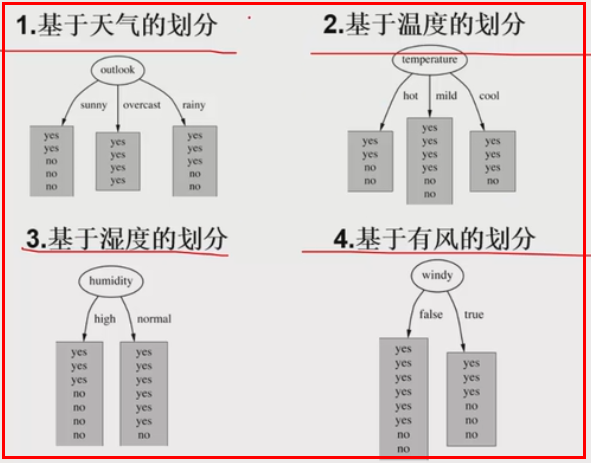
信息增溢值越大越好


谁当根节点？








信息增益率


重要：


												


											
Jike_Time-决策树的更多相关文章
	

    
						
  1. 使用python抓取婚恋网用户数据并用决策树生成自己择偶观
		
    最近在看<机器学习实战>的时候萌生了一个想法,自己去网上爬一些数据按照书上的方法处理一下,不仅可以加深自己对书本的理解,顺便还可以在github拉拉人气.刚好在看决策树这一章,书里面的理论 ...
    
		
    2. 
						
  2. 【Machine Learning】决策树案例：基于python的商品购买能力预测系统
		
    决策树在商品购买能力预测案例中的算法实现 作者:白宁超 2016年12月24日22:05:42 摘要:随着机器学习和深度学习的热潮,各种图书层出不穷.然而多数是基础理论知识介绍,缺乏实现的深入理解.本 ...
    
		
    3. 
						
  3. 决策树ID3算法的java实现(基本试用所有的ID3)
		
    已知:流感训练数据集,预定义两个类别: 求:用ID3算法建立流感的属性描述决策树 流感训练数据集 No. 头痛 肌肉痛 体温 患流感 1 是(1) 是(1) 正常(0) 否(0) 2 是(1) 是(1 ...
    
		
    4. 
						
  4. 决策树及R语言实现
		
    决策树是什么 决策树是基于树结构来进行决策,这恰是人类在面临决策问题时一种很自然的处理机制.例如,我们要对"这是好瓜吗?"这样的问题进行决策时,通常会进行一系列的判断或" ...
    
		
    5. 
						
  5. 决策树-ID3
		
    id3:无法直接处理数值型数据,可以通过量化方法将数值型数据处理成标称型数据,但涉及太多特征划分,不建议 决策树:的最大优点在于可以给出数据的内在含义,数据形式非常容易理解: 决策树介绍:决策树分类器 ...
    
		
    6. 
						
  6. python画决策树
		
    1.安装graphviz.下载地址在:http://www.graphviz.org/.如果你是linux,可以用apt-get或者yum的方法安装.如果是windows,就在官网下载msi文件安装. ...
    
		
    7. 
						
  7. MLlib决策树与集成树
		
    决策树是一种常见的分类与回归机器学习算法,由于其模型表达性好,便于理解,并能取得较好的效果,而受到广泛的应用.下图是一个简单的决策树,决策树每个非叶子节点包含一个条件,对于具有连续值的特征,该条件为一 ...
    
		
    8. 
						
  8. 决策树和基于决策树的集成方法（DT,RF,GBDT,XGBT）复习总结
		
    摘要: 1.算法概述 2.算法推导 3.算法特性及优缺点 4.注意事项 5.实现和具体例子 内容: 1.算法概述 1.1 决策树(DT)是一种基本的分类和回归方法.在分类问题中它可以认为是if-the ...
    
		
    9. 
						
  9. Spark中决策树源码分析
		
    1.Example 使用Spark MLlib中决策树分类器API,训练出一个决策树模型,使用Python开发. """ Decision Tree Classifica ...
    
		
    10. 
						
  10. [Machine Learning & Algorithm] 决策树与迭代决策树（GBDT）
		
    谈完数据结构中的树(详情见参照之前博文<数据结构中各种树>),我们来谈一谈机器学习算法中的各种树形算法,包括ID3.C4.5.CART以及基于集成思想的树模型Random Forest和G ...
    
		
    11. 
		

	


随机推荐
	

    
									
  1. Mysql 如何创建一张临时表
			
    mysql 利用 temporary 关键字就可以创建出一个临时表.创建的这张表会在与服务器的会话终止时自动消失 语法:create temporary table tbl_name...; 规则:每 ...
    
			
    2. 
						
  2. POI2008 CLO-Toll
			
    [POI2008]CLO-Toll 题意描述 Byteotia城市有n个 towns m条双向roads. 每条 road 连接 两个不同的 towns ,没有重复的road. 你要把其中一些road ...
    
			
    3. 
						
  3. AJAX 实现form表单提交
			
    1.使用Ajax实现异步操作,点击登录按钮后,即触发form表单的提交事件,数据传输至后端 JSP: <script type="text/javascript" src=& ...
    
			
    4. 
						
  4. C#开发BIMFACE系列28 服务端API之获取模型数据13：获取三维视点或二维视图列表
			
    系列目录     [已更新最新开发文章,点击查看详细] 本篇主要介绍如何获取一个模型中包含的三维视点或二维视图列表. 请求地址:GET https://api.bimface.com/data/v2/ ...
    
			
    5. 
						
  5. golang数据结构之栈
			
    stack.go package stack import ( "errors" "fmt" ) type Stack struct { MaxTop int  ...
    
			
    6. 
						
  6. workbook数据相关操作
			
    访问单个单元格 c = ws['A4'] #返回单元格A4,如果单元格不存在,则会自动创建 ws['A4'] = 4 #为单元格A4赋值为4 d = ws.cell(row=4, column=2,  ...
    
			
    7. 
						
  7. JavaScript判断对象和数组
			
    在调用后端接口时,由于后端接口的不规范统一,接口最外层在没有数据时返回的是空数组(其实更想要的是空json对象,接口返回的data数据应该统一返回json对象,便于扩展),而在有数据时返回的是json ...
    
			
    8. 
						
  8. 常见跨域解决方案以及Ocelot 跨域配置
			
    常见跨域解决方案以及Ocelot 跨域配置 Intro 我们在使用前后端分离的模式进行开发的时候,如果前端项目和api项目不是一个域名下往往会有跨域问题.今天来介绍一下我们在Ocelot网关配置的跨域 ...
    
			
    9. 
						
  9. windows环境下安装配置MongoDB
			
    版本选择MongoDB的版本命名规范如:x.y.z: y为奇数时表示当前版本为开发版,如:2.3.0.2.1.1: y为偶数时表示当前版本为稳定版,如:2.0.1.2.2.0: 目前官网上最新的版本为 ...
    
			
    10. 
						
  10. Python入门你要懂哪些？
			
    前言 什么是计算机语言 计算机就是一台用来计算的机器,人让计算机干什么计算机就得干什么! 需要通过计算机的语言来控制计算机(也就是编程语言)! 计算机语言其实和人类的语言没有本质的区别,不同点就是交流 ...
    
			
    11.