洛谷 P2254 [NOI2005]瑰丽华尔兹（单调栈优化DP）

题目描述

不妨认为舞厅是一个N行M列的矩阵，矩阵中的某些方格上堆放了一些家具，其他的则是空地。钢琴可以在空地上滑动，但不能撞上家具或滑出舞厅，否则会损坏钢琴和家具，引来难缠的船长。每个时刻，钢琴都会随着船体倾斜的方向向相邻的方格滑动一格，相邻的方格可以是向东、向西、向南或向北的。而艾米丽可以选择施魔法或不施魔法：如果不施魔法，则钢琴会滑动；如果施魔法，则钢琴会原地不动。

艾米丽是个天使，她知道每段时间的船体的倾斜情况。她想使钢琴在舞厅里滑行的路程尽量长，这样1900 会非常高兴，同时也有利于治疗托尼的晕船。但艾米丽还太小，不会算，所以希望你能帮助她。

输入格式

输入文件的第一行包含5个数N, M, x, y和K。N和M描述舞厅的大小，x和y为钢琴的初始位置；我们对船体倾斜情况是按时间的区间来描述的，且从1开始计算时间，比如“在[1, 3]时间里向东倾斜，[4, 5]时间里向北倾斜”，因此这里的K表示区间的数目。

以下N行，每行M个字符，描述舞厅里的家具。第i 行第j 列的字符若为‘ . ’，则表示该位置是空地；若为‘ x ’，则表示有家具。

以下K行，顺序描述K个时间区间，格式为：si ti di(1 ≤ i ≤ K)。表示在时间区间[si, ti]内，船体都是向di方向倾斜的。di为1, 2, 3, 4中的一个，依次表示北、南、西、东（分别对应矩阵中的上、下、左、右）。输入保证区间是连续的，即

s1 = 1 ti = si-1 + 1 (1 < i ≤ K)

tK = T

输出格式

输出文件仅有1行，包含一个整数，表示钢琴滑行的最长距离(即格子数)。

输入输出样例

输入 #1复制

4 5 4 1 3
..xx.
.....
...x.
.....
1 3 4
4 5 1
6 7 3

输出 #1复制

6

说明/提示

钢琴的滑行路线：

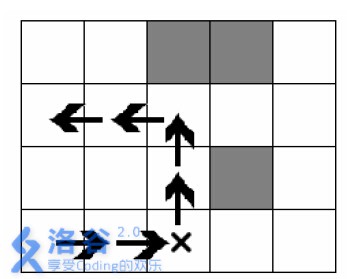
钢琴在“×”位置上时天使使用一次魔法，因此滑动总长度为6。

【数据范围】

50%的数据中，1≤N, M≤200，T≤200；

100%的数据中，1≤N, M≤200，K≤200，T≤40000。

---

题意：题目说的很清楚，就是给你一张图有空'.',有障碍'x',钢琴起始位置在sx,sy,给你K个输入，表示钢琴在时间s到t可以向d方向滑动，但是你可施加魔法，是的钢琴在某个时间不滑动，问你钢琴最多可以滑动多少格；

题解：首先考虑对于时间t来dp： f[t][i][j]表示在第t时刻在第i行第j列所能获得的最长距离。 转移方程：f[t][i][j]=max(f[t-1][i][j],f[t][i*][j*]+1)(i*,j*为上一个合理的位置) 但对于100%TLE且MLE。 所以必须优化，首先把时间t换成区间k， 令f[k][i][j]表示在第k段滑行区间中在位置i，j所能获得最长距离 注意到在第k段时间内只能向某个方向最多走x步（x为区间长度），得到转移方程 f[k][i][j]=max(f[k-1][i][j],f[k][i*][j*]+dis(i,j,i*,j*))(i*,j*为上一个合理的位置) 这个做法的时间复杂度是O(kn^3)，会超时，需要进一步优化 用单调队列优化掉内层的一个n，就可以做到O(kn^2)，可以AC，本代码中还使用了滚动数组优化 用单调递减队列求最大值时，遇到障碍清空整个队列即可，另外队列比较时需要加上偏移量dis。

参考代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pii pair<int,int>
#define pil pair<int,ll>
#define mkp make_pair
#define fi first
#define se second
const int INF=0x3f3f3f3f;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-') f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=(x<<)+(x<<)+ch-'';ch=getchar();}
    return x*f;
}
const int maxn=;
pii q[maxn];
int n,m,sx,tx,K,ans,dp[maxn][maxn];
char G[maxn][maxn];
int dx[]={,-,,,},dy[]={,,,-,};
inline void work(int x,int y,int len,int d)
{
    int l=,r=;
    for(int i=;x>=&&x<=n&&y>=&&y<=m;++i,x+=dx[d],y+=dy[d])
    {
        if(G[x][y]=='x') l=r=;
        else
        {
            while(l<r&&q[r-].fi+i-q[r-].se<dp[x][y]) --r;
            q[r++]=mkp(dp[x][y],i);
            if(q[r-].se-q[l].se>len) ++l;
            dp[x][y]=q[l].fi+i-q[l].se;
            ans=max(ans,dp[x][y]);
        }
    }
}
int main()
{
    n=read();m=read();sx=read();tx=read();K=read();
    for(int i=;i<=n;++i) scanf("%s",G[i]+);
    memset(dp,-INF,sizeof dp);
    dp[sx][tx]=;
    for(int j=;j<=K;++j)
    {
        int s,t,d,len;
        s=read();t=read();d=read();
        len=t-s+;
        if(d==) for(int i=;i<=m;++i) work(n,i,len,d);
        if(d==) for(int i=;i<=m;++i) work(,i,len,d);
        if(d==) for(int i=;i<=n;++i) work(i,m,len,d);
        if(d==) for(int i=;i<=n;++i) work(i,,len,d);
    }
    printf("%d\n",ans);

    return ;
}