Repeats SPOJ - REPEATS（重复次数最多的连续重复子串）

论文题例8

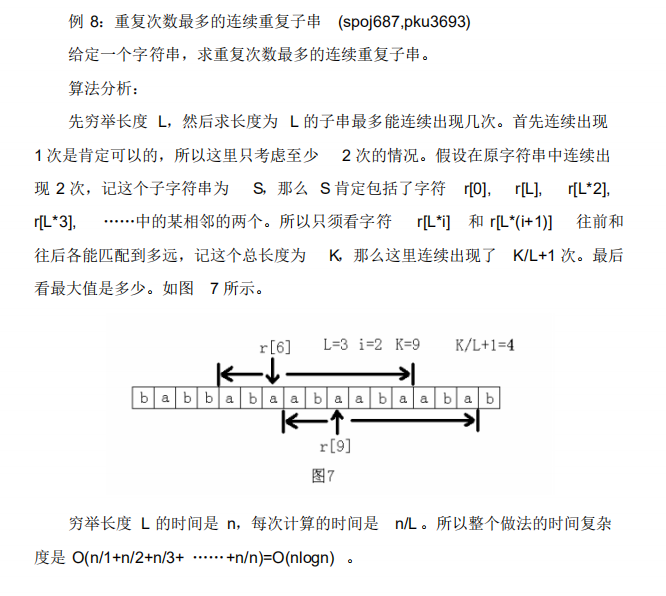
https://blog.csdn.net/queuelovestack/article/details/53031731这个解释很好

其实，当枚举的重复子串长度为i时，我们在枚举r[i*j]和r[i*(j+1)]的过程中，必然可以出现r[i*j]在第一个重复子串里，而r[i*(j+1)]在第二个重复子串里的这种情况，如果此时r[i*j]是第一个重复子串的首字符，这样直接用公共前缀k除以i并向下取整就可以得到最后结果。但如果r[i*j]如果不是首字符，这样算完之后结果就有可能偏小，因为r[i*j]前面可能还有少许字符也能看作是第一个重复子串里的。
于是，我们不妨先算一下，从r[i*j]开始，除匹配了k/i个重复子串，还剩余了几个字符，剩余的自然是k%i个字符。如果说r[i*j]的前面还有i-k%i个字符完成匹配的话，这样就相当于利用多余的字符还可以再匹配出一个重复子串，于是我们只要检查一下从r[i*j-(i-k%i)] （前缀首字符位置）和r[i*(j+1)-(i-k%i)]开始是否有i-k%i个字符能够完成匹配即可，也就是说去检查这两个后缀的最长公共前缀是否比i-k%i大即可。
当然如果公共前缀不比i-k%i小，自然就不比i小，因为后面的字符都是已经匹配上的，所以为了方便编写，程序里面就直接去看是否会比i小就可以了。

用了rmq区间最小来求 位置i*j的前缀 和 i*j+1位置的前缀的最长公共前缀

//为什么这样能求出重复次数最多的连续重复子串  请先搞懂next循环节求连续重复子串 这题就懂了https://www.cnblogs.com/WTSRUVF/p/9461066.html

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff;
int s[maxn];
int sa[maxn], t[maxn], t2[maxn], c[maxn], n;
int ran[maxn], height[maxn];
int d[][];

void get_sa(int m)
{
    int i, *x = t, *y = t2;
    for(i = ; i < m; i++) c[i] = ;
    for(i = ; i < n; i++) c[x[i] = s[i]]++;
    for(i = ; i < m; i++) c[i] += c[i-];
    for(i = n-; i >= ; i--) sa[--c[x[i]]] = i;
    for(int k = ; k <= n; k <<= )
    {
        int p = ;
        for(i = n-k; i < n; i++) y[p++] = i;
        for(i = ; i < n; i++) if(sa[i] >= k) y[p++] = sa[i] - k;
        for(i = ; i < m; i++) c[i] = ;
        for(i = ; i < n; i++) c[x[y[i]]]++;
        for(i = ; i< m; i++) c[i] += c[i-];
        for(i = n-; i >= ; i--) sa[--c[x[y[i]]]] = y[i];
        swap(x, y);
        p = ; x[sa[]] = ;
        for(i = ; i < n; i++)
            x[sa[i]] = y[sa[i-]] == y[sa[i]] && y[sa[i-]+k] == y[sa[i]+k] ? p- : p++;
        if(p >= n) break;
        m = p;
    }
    int k = ;
    for(i = ; i < n; i++) ran[sa[i]] = i;
    for(i = ; i < n; i++)
    {
        if(k) k--;
        int j = sa[ran[i]-];
        while(s[i+k] == s[j+k]) k++;
        height[ran[i]] = k;
    }
}

void rmq_init()
{
    for(int i=; i<n; i++) d[i][] = height[i];
    for(int j=; (<<j) <= n; j++)
        for(int i=; i+(<<j)- < n; i++)
            d[i][j] = min(d[i][j-], d[i+(<<(j-))][j-]);
}

int rmq(int l, int r)
{
    int k = ;
    while((<<(k+)) <= r-l+) k++;
    return min(d[l][k], d[r-(<<k)+][k]);
}

int  qp(int l, int r)
{
    l = ran[l], r = ran[r];
    if(l > r) swap(l, r);
    return rmq(l+, r);         //因为height里是等级i和i-1的最长公共前缀 所以是l+1 不然就越界了
}

int T;
char str[];
int main()
{
    rd(T);
    while(T--)
    {
        n = ;
        int q;
        rd(q);
        rep(i, , q)
        {
            rs(str);
            s[n++] = str[] - 'a' + ;
        }
        s[n++] = ;
        get_sa();
        rmq_init();
        int maxx = -INF, ans;
        for(int i=; i<=n; i++)
        {
            for(int j=; j+i<n; j+=i)
            {
                ans = qp(j, j+i);
                int k = j - (i - ans%i);
                ans = ans/i + ;        //因为j+i的后缀突出来一段长为i的串 所以+1
                if(k>= && qp(k, k+i) >= i)
                    ans++;
                maxx = max(maxx, ans);
            }
        }
        cout<< maxx <<endl;
    }

    return ;
}