树形dp（B - Computer HDU - 2196 ）

题目链接：https://cn.vjudge.net/contest/277955#problem/B

题目大意：首先输入n代表有n个电脑，然后再输入n-1行，每一行输入两个数，t1,t2.代表第（i+1）个电脑连向电脑t1，花费是t2，然后问你每个电脑的到其他电脑的最大花费。

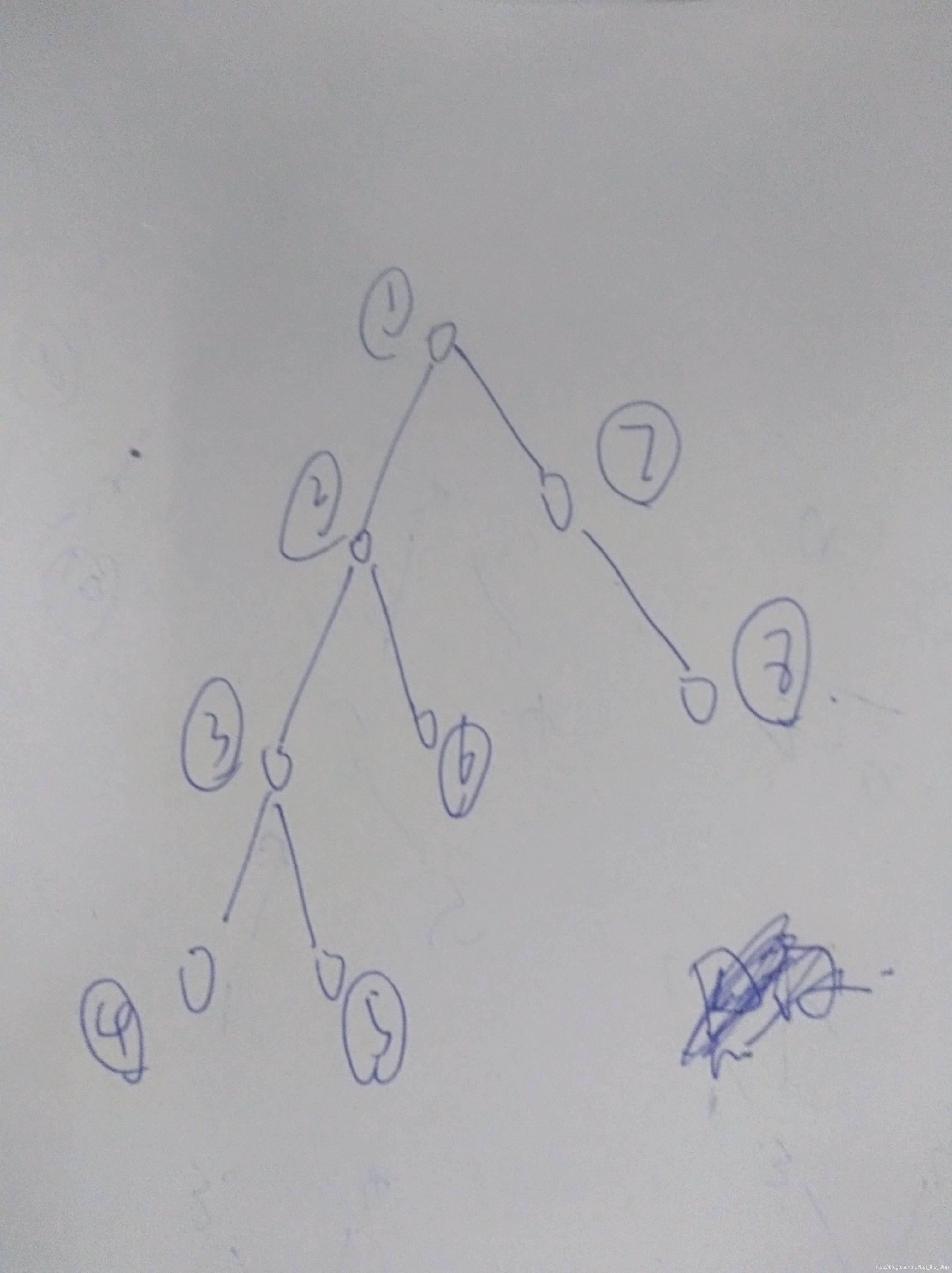
具体思路：按照图来想，对于节点2，最大的花费的路径可能有两种，第一种，往下遍历他的叶子节点找到最大的，第二种，先往上走，然后从往上走的节点再去找最大的花费。

对于第一种花费，我们直接dfs求就可以了。 但是在求的时候顺便求一下当前这个节点往下的第二大花费，具体作用是在第二种情况中会使用到。

对于第二种花费，我们先是往上移动，然后再去求他上面的点的最大花费，但是这个地方要注意一点，在往上面走的时候，求的最小花费可能会有路径重复，比如说三号节点，往上走的话是2号节点，而二号节点的最远距离有可能是2->3->4，这样的话，就会有一段路径重复计算。这个时候求的次小花费就能有用处了，既然我花费最大的用不了，那么我就用花费第二小的。

状态转移方程： 对于第二种情况,如果当前的节点的父亲节点的最大花费的路径中包括当前这个节点，这个时候我们就算上第二大的，然后再加上当前这个点到父亲节点的花费就可以了。否则就安最大花费计算。

AC代码：

 #include<iostream>
 #include<cmath>
 #include<stack>
 #include<stdio.h>
 #include<algorithm>
 #include<queue>
 #include<vector>
 #include<cstring>
 using namespace std;
 # define inf 0x3f3f3f3f
 # define ll long long
 const int maxn = 4e4+;
 struct node
 {
     int nex;
     int to;
     int cost;
 } edge[maxn];
 int num,head[maxn],dp[maxn][],father[maxn];
 void init()
 {
     num=;
     memset(head,-,sizeof(head));
     memset(dp,,sizeof(dp));
 }
 void addedge(int fr,int to,int cost)
 {
     edge[num].to=to;
     edge[num].nex=head[fr];
     edge[num].cost=cost;
     head[fr]=num++;
 }
 void dfs1(int st,int rt)
 {
     for(int i=head[st]; i!=-; i=edge[i].nex)
     {
         int to=edge[i].to;
         if(to==rt)
             continue;
         dfs1(to,st);
         if(dp[to][]+edge[i].cost>dp[st][])
         {
             father[st]=to;// 这个地方要注意是谁是数组的下标，我们需要判断的是这个父亲节点的路径上是不是包括这个子节点。
             dp[st][]=dp[st][];//记录次大的
             dp[st][]=dp[to][]+edge[i].cost;
         }
         else if(dp[to][]+edge[i].cost>dp[st][])
         {
             dp[st][]=dp[to][]+edge[i].cost;
         }
     }
 }
 void dfs2(int st,int rt)
 {
     for(int i=head[st]; i!=-; i=edge[i].nex)
     {
         int to=edge[i].to;
         if(to==rt)
             continue;
         if(father[st]==to)
         {
             dp[to][]=max(dp[st][],dp[st][])+edge[i].cost;
         }
         else
             dp[to][]=max(dp[st][],dp[st][])+edge[i].cost;
         dfs2(to,st);
     }
 }
 int main()
 {
     int n;
     while(~scanf("%d",&n))
     {
         init();
         int t1,t2;
         for(int i=; i<=n; i++)
         {
             scanf("%d %d",&t1,&t2);
             addedge(i,t1,t2);
             addedge(t1,i,t2);
         }
         dfs1(,-);
         dfs2(,-);
         for(int i=; i<=n; i++)
         {
             printf("%d\n",max(dp[i][],dp[i][]));
         }
     }
     return ;
 }