hdu2571 命运 2016-09-11 16:54 53人阅读 评论(0) 收藏

命运

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 16889    Accepted Submission(s): 5888

Problem Description

穿过幽谷意味着离大魔王lemon已经无限接近了！

可谁能想到，yifenfei在斩杀了一些虾兵蟹将后，却再次面临命运大迷宫的考验，这是魔王lemon设下的又一个机关。要知道，不论何人，若在迷宫中被困1小时以上，则必死无疑！

可怜的yifenfei为了去救MM，义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧！

命运大迷宫可以看成是一个两维的方格阵列，如下图所示：

 

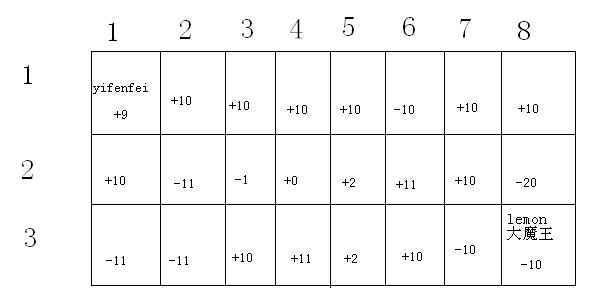
yifenfei一开始在左上角，目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒，所以每个格子都对应一个值，走到那里便自动得到了对应的值。

现在规定yifenfei只能向右或者向下走，向下一次只能走一格。但是如果向右走，则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子，即：如果当前格子是（x,y），下一步可以是（x+1,y），(x,y+1)或者(x,y*k) 其中k>1。 

为了能够最大把握的消灭魔王lemon，yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。

 

Input

输入数据首先是一个整数C，表示测试数据的组数。

每组测试数据的第一行是两个整数n,m，分别表示行数和列数(1<=n<=20,10<=m<=1000)；

接着是n行数据，每行包含m个整数，表示n行m列的格子对应的幸运值K ( |k|<100 )。

 

Output

请对应每组测试数据输出一个整数，表示yifenfei可以得到的最大幸运值。

 

Sample Input

1
3 8
9 10 10 10 10 -10 10 10
10 -11 -1 0 2 11 10 -20
-11 -11 10 11 2 10 -10 -10

 

Sample Output

52

 

Author

yifenfei

 

题目是经典的dp模型，每一步都可能来自dp[i-1][j],dp[i][j-1],dp[i][k](k是j的因子不包括自己)，对于因子的处理，直接暴力搜一遍好了，找出这些中的最大值mx；dp[i][j]=mx+mp[i][j]

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <stack>
#include <queue>
#include <algorithm>
using namespace std;
#define inf 0x3f3f3f3f

int dp[25][1005];
int mp[25][1005];
int m,n;

int main()
{
    int o,mx;
    while(~scanf("%d",&o))
    {
        while(o--)
        {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++)
            scanf("%d",&mp[i][j]);
        memset(dp,0,sizeof(dp));
     dp[1][1]=mp[1][1];
     for(int i=2;i<=m;i++)
     {
         mx=-1000;
         for(int j=1;j<i;j++)
     {
         if(i%j==0)
            mx=max(mx,dp[1][j]);
     }
     mx=max(mx,dp[1][i-1]);
     dp[1][i]=mx+mp[1][i];
     }

     for(int i=2;i<=n;i++)
     {
         dp[i][1]=dp[i-1][1]+mp[i][1];
     }

     for(int i=2;i<=n;i++)
        for(int j=2;j<=m;j++)
     {
         mx=-1000;
         mx=max(mx,dp[i-1][j]);
         mx=max(mx,dp[i][j-1]);
         for(int k=1;k<j;k++)
         {
             if(j%k==0)
                mx=max(mx,dp[i][k]);
         }
         dp[i][j]=mx+mp[i][j];
     }

     printf("%d\n",dp[n][m]);
        }
    }
    return 0;
}