PCA，到底在做什么

很久以前写过一篇 PCA 的小白教程，不过由于当时对 PCA 的理解流于表面，所以只是介绍了一下 PCA 的算法流程。今天在数图课上偶然听到 PCA 在图像压缩上的应用，突然明白了一点实质性的东西，这里趁热记录一波。

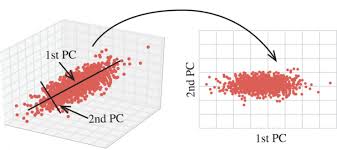
PCA 算法

首先还是简单回顾下 PCA 的算法流程。

我们把样本数据 \(x\) 归一化后，计算其协方差矩阵 \(C_x\)，然后计算 \(C_x\) 的特征向量，构造出一个特征向量矩阵 \(A\)，最后把 \(x\) 通过该矩阵映射到一个新的空间，得到的向量 \(y\) 就是能体现 \(x\) 主要成分的向量了。

PCA 在做什么

那么，这种空间映射有什么意义呢？问题要回到协方差矩阵 \(C_x\) 上。我们知道，协方差矩阵是一个对称矩阵，在线性代数中，对称矩阵的特征向量是相互正交的。而我们把 \(x\) 通过这个特征向量矩阵映射到 \(y\)，其实就是把原来的数据由最初的 \([e_1, e_2, \dots, e_n]\) 的单位坐标系，调整到这些正交的特征向量组成的坐标系下，如下图所示：

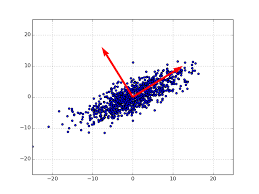
这种坐标变换的意义又在哪呢？

如果仔细分析，我们就会发现，这些新得到的向量 \(y\) 的均值为 \(0\)，而且它们的协方差矩阵为：
\[
C_y=AC_xA^T=\begin{bmatrix} \lambda_1 & & & 0 \\ & \lambda_2 & & \\ & & \ddots & \\ 0 & & & \lambda_n \end{bmatrix}
\]
这里，\(A\) 是由 \(C_x\) 的特征向量组成的矩阵，它的第一行表示最大特征值对应的特征向量，第二行表示第二大特征值对应的特征向量。\(C_y\) 对角线上的 \(\lambda_k\) 代表 \(C_x\) 的特征值，而且是按照从大到小排序的（\(\lambda_1 > \lambda_2 > \dots > \lambda_n\)）。

这个新的协方差矩阵有一个很重要的性质，除了对角线上的元素，其他元素通通是 0。要知道，协方差矩阵中，对角线上的元素表示方差，非对角线上的元素表示协方差。这说明，经过 PCA 处理后，我们把原本的数据 \(x\)，转变成各个分量之间没有任何关系（协方差为 0）的数据 \(y\)！我认为这正是 PCA 的精髓所在，也是我们使用 PCA 算法的根本目标。

另外，PCA 还经常用于降维处理，那么为什么 PCA 的降维效果会那么好？

首先要明确一点，降维不是随便都能降的，最好的降维方法是要尽量保留重要的信息，而忽略次要的信息。在 PCA 中，我们一般是对协方差矩阵的特征值按从大到小排序，然后舍弃一些比较小的特征值（以及这些特征值对应的特征向量），这样重新计算得到 \(y\) 后，它的协方差矩阵可能是这个样子的：
\[
C_y=\begin{bmatrix} \lambda_1 & & & 0 \\ & \lambda_2 & & \\ & & \ddots & \\ 0 & & & \lambda_k \end{bmatrix}
\]
（我们舍弃掉了 \(n-k\) 个特征向量，将数据由 \(n\) 维降到 \(k\) 维）

要知道，这些特征值（或者说方差）都是按照从大到小排序的，也就是说，我们在降维时，舍弃掉了那些特征值比较小的分量。这么做是符合常理的，因为数据的方差越大，证明分布越广，这样，我们还原这些数据的难度是越大的，而方差越小，证明数据分布越集中，还原它们的难度就越小（方差为 0 的话，用一个数就可以代表所有样本了）。所以，降维时，我们尽量保留那些方差大的数据，而忽略那些方差小的。本文开篇的图中给出一个形象的解释，我们把一个二维的数据映射到一维时，也是优先映射到方差大的那一维上，这样，原数据的分布规律可以最大限度的保留下来，信息的保留也是最完整的。