1120 机器人走方格 V3（组合数）

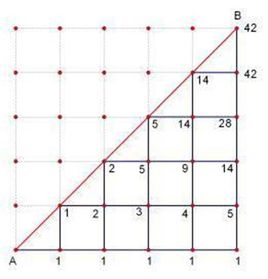
题目实际上是求catalan数的，Catalan[n] = C(2*n,n) / (n+1) = C(2*n,n) % mod * inv[n+1],inv[n+1]为n+1的逆元，根据费马小定理，可以通过快速幂快速求出。

因为n的数据范围较大，所以要用到卢卡斯定理：若p为素数，那么C(m,n)%p = C(m/p,n/p) * C(m%p,n%p)  % p.从而我们可以递归的可以求出C(m,n)，当n==0，返回1.

因为方格含有两个三角形，所以Catalan[n]*2 即是最终答案

#include<stdio.h>
#include<math.h>
#include<vector>
#include<stack>
#include<set>
#include<string.h>
#include<iostream>
#include<algorithm>
#define MAXSIZE 10005
#define INF 0x3f3f3f3f
using namespace std;
#define LL long long
const LL mod = 1e4+;
LL inv[mod+];

LL Pow(LL n,LL m)
{
    n %= mod;
    LL ans = ;
    while(m>)
    {
        if(m%)
            ans = (ans*n)%mod;
        n = (n*n)%mod;
        m /= ;
    }
    return ans;
}

LL C(LL m,LL n) //对mod取模后,m,n的值均小于1e4+7，直接求组合即可
{
    if(n > m)
        return ;
    LL ans = ;
    for(int i=; i<=n; i++)
    {
        ans = ans*(m-i+)%mod*inv[i]%mod;
    }
    return ans;
}

LL Lucas(LL n, LL m) //卢卡斯定理
{
    if(m==)
        return ;
    return Lucas(n/mod,m/mod)%mod*C(n%mod,m%mod)%mod;
}

LL Solve(LL n)
{
    LL ans = Lucas(*n,n)%mod;
    LL Inv = Pow(n+,mod-); //inv(n+1)
    ans = ans%mod*Inv%mod;
    return ans *  % mod;
}

int main()
{
    for(int i=; i<=mod; i++)
        inv[i] = Pow(i,mod-); //预处理求出逆元
    LL n;
    scanf("%lld",&n);
    LL ans = Solve(n-);
    printf("%lld\n",ans);
    return ;
}