react中的路由配置踩坑记

react 路由配置中，如果根路由（/）匹配一个组件，另一个路由（/list）在进行匹配的时候也会匹配到根路由（/），即在 /list 页面展示的时候 / 页面总是展示在上方。

此时如果想进行严格匹配，有两种实现方式：

1、在 / 路由配置中使用 exact， 这时候在匹配 /list 时候， / 页面不会显示。

2、去除了exact之后，无论进哪个页面都是“/”对应的页面，这个时候，只需要把路由的顺序调整一下，把“/”这个Route放到最后即可

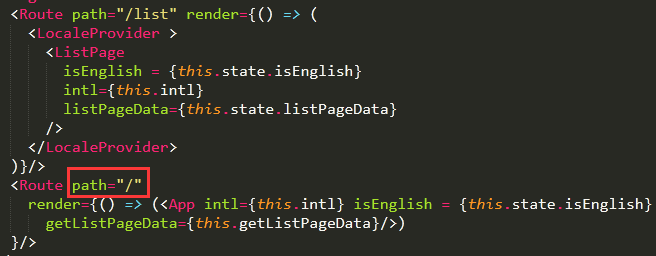
注意事项：

react-router 嵌套路由 内层route找不到。

exact精确匹配

<Route component={xxx} path="/" />

　路径为“/”的时候用了exact精确查找，所以不会查找到页面的嵌套路由