BZOJ1951 [Sdoi2010]古代猪文 中国剩余定理 快速幂 数论

原文链接http://www.cnblogs.com/zhouzhendong/p/8109156.html

---

题目传送门 - BZOJ1951

---

题意概括

　　求 G^M mod 999911659

　　M=∑_i|nC(n,i)

　　N,G<=10⁹

---

题解

　　我们发现999911659是一个素数，设为p。

　　费马小定理：对于任意正整数a，和素数p，有

　　　　　　　　　　　　　　　　　　　　　a^p-1 Ξ 1 (mod p)

　　由此可得，　　　　　　　　　　　　　　G^M Ξ G^{M mod (p-1)} (mod p)

　　这个可以用快速幂搞定，现在的问题就是如何计算M

　　我们研究p-1这个数。

　　我们把他分解质因数：

　　p-1 = 999911658 = 2 × 3 × 4679 × 35617

　　我们发现他们都很小。而且没有质数的多次方之类的（不然貌似要用到ex_lucas）

　　我们于是分组解决这个问题。

　　对于模数为2、3、4679、35617我们分别求解。

　　设当前的模数为p，那么，我们只需要枚举i(i|n)，可以在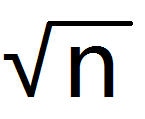的复杂度里面得到所有的i，那么现在我们考虑计算C(n,i)。

　　显然，这个可以套Lucas定理：（设p为当前的素模数）

　　　　　　　　　　　　　C(n,m) Ξ C(n mod p,m mod p) × C(n div p,m div p)   (mod p)

　　于是我们可以将n和m的规模在log的复杂度内搞到p以下。然后直接套C函数的公式就可以了（提前预处理出阶乘）。

　　那么，我们得到了4个答案。

　　然后我们考虑结合4个答案。

　　记我们的答案分别为a[0]、a[1]、a[2]、a[3]；而之前的四个数为p[0]~p[4]。

　　我们发现，我们得到的4个答案可以写出等式：

　　　　　　　　　　　　　　　　　　a[i] Ξ M (mod p[i])   (0<=i<4)

　　 这个很明显就是中国剩余定理（CRT）可以搞定的。

　　而且p[i]都是质数，两两互质，那么就更好办了。

　　注意，开始的时候要把G=999911659的情况判掉，不然会出错。

---

代码

#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef long long LL;
LL mod=999911659;
LL num[4]={2,3,4679,35617};
LL N,G,M,a[4];
LL Pow(LL x,LL y,LL mod){
	if (!y)
		return 1LL;
	LL xx=Pow(x,y/2,mod);
	xx=xx*xx%mod;
	if (y&1LL)
		xx=xx*x%mod;
	return xx;
}
LL Inv(LL x,LL mod){
	return Pow(x,mod-2,mod);
}
LL fac[4][36000],inv[4][36000];
void Get_fac(){
	for (LL x=0;x<4;x++){
		fac[x][0]=1;
		for (LL i=1;i<num[x];i++)
			fac[x][i]=fac[x][i-1]*i%num[x];
	}
	for (LL x=0;x<4;x++)
		for (LL i=0;i<num[x];i++)
			inv[x][i]=Inv(fac[x][i],num[x]);
}
LL _C(int i,LL N,LL M){
	if (N<M)
		return 0;
	return fac[i][N]*inv[i][M]%num[i]*inv[i][N-M]%num[i];
}
LL C(int i,LL N,LL M){
	if (M==0)
		return 1LL;
	return _C(i,N%num[i],M%num[i])*C(i,N/num[i],M/num[i])%num[i];
}
void ex_gcd(LL a,LL b,LL &x,LL &y){
	if (b==0){
		x=1,y=0;
		return;
	}
	ex_gcd(b,a%b,y,x);
	y-=(a/b)*x;
}
LL CRT(){
	LL x,y,A=num[0],B=a[0];
	for (int i=1;i<4;i++){
		LL A1=num[i],B1=a[i];
		ex_gcd(A,A1,x,y);
		x=((B1-B)*x%A1+A1)%A1;
		B+=A*x;
		A*=A1;
	}
	return B;
}
int main(){
	scanf("%lld%lld",&N,&G);
	if (G==mod){
		puts("0");
		return 0;
	}
	Get_fac();
	for (LL x=0;x<4;x++)
		for (LL i=1;i<=(LL)sqrt(N);i++)
			if (N%i==0){
				int A=i,B=N/i;
				if (A!=B)
					a[x]=(a[x]+C(x,N,A)+C(x,N,B))%num[x];
				else
					a[x]=(a[x]+C(x,N,i))%num[x];
			}
	LL res=CRT();
	printf("%lld",Pow(G,res,mod));
	return 0;
}