1  不理解等一个等式 ，
2.不理解为什么，一个可分的集合里面有不可数的子集？谢谢

1是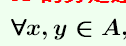

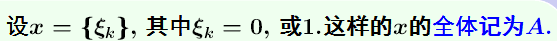
2.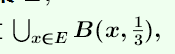是可分集合里面每个元素 做中心后的一个开覆盖

所有0 1序列是和所有二进制小数   可以一一对应   而所有二进制小数可以和[0,1]闭区间一一对应

所以不可数

l^oo不可分的两个注意点的更多相关文章

  1. hdu 4630 查询[L,R]区间内任意两个数的最大公约数

    No Pain No Game Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) ...

  2. CodeForces 1098F. Ж-function

    题目简述:给定字符串$s[1 \dots n](n \leq 2 \times 10^5)$,以及$Q \leq 2 \times 10^5$个询问,每个询问有两个参数$1 \leq l \leq r ...

  3. L​i​n​u​x​环​境​变​量​的​设​置​和​查​看​方​法

    L​i​n​u​x​环​境​变​量​的​设​置​和​查​看​方​法 1. 显示环境变量HOME [root@AY1404171530212980a0Z ~]# echo $HOME /root 2. ...

  4. js实现继承的两种方式

    这是面试时面试官会经常问到问题: js的继承方式大致可分为两种:对象冒充和原型方式: 一.先说对象冒充,又可分为3种:临时属性方式.call().apply(): 1.临时属性方式: 当构造对象son ...

  5. Spring 的两个配置容器的讲解

    容器 是Spring框架的核心,是组件存活的地方.Spring容器使用DI管理所有组成应用系统的组件,协作组件之间建立联.而且, 这些对象简洁易懂,降低耦合性,支持重用,容易被测试. Spring提供 ...

  6. 最近两场比赛 CF 285 & TC 646

    Codeforces 285 这场rating又掉了,好在只掉了十多. 题目比较水,但是我比赛时居然只艰辛地过了前两道. 504A 由于图是森林,所以一定有度为1的点,把这些点删了后图还是森林.然后就 ...

  7. C语言 字符串前加L的意义 如：L“A”

    转自:http://c.biancheng.net/cpp/html/1069.html Unicode或者宽字符都没有改变char数据型态在C中的含义.char继续表示1个字节的储存空间,sizeo ...

  8. 证明与计算(1): Decision Problem, Formal Language L, P and NP

    0x01 从判定问题到形式语言 这篇讲知识证明的wiki([1]): https://en.wikipedia.org/wiki/Proof_of_knowledge 里面有一句话: Let x be ...

  9. Linux rsync 两个目录镜像备份

    rsync安装篇 rsync是一款配置简单,功能全面的安全备份软件,具体的功能介绍可以参考手册.这里和大家分享一下rsync在CentOS下的部署. 1.安装rsync,并通过xinetd管理rsyn ...

随机推荐

  1. Stopwatch + C#打印日志方法

    打印一个接口.方法的运行时间在程序中是很容易遇到的一件事情:现在,我就分享一个我在工作中使用的临时打印日志的方法和结合 Stopwatch 打印测量某个时间间隔的运行时间的方法. Stopwatch ...

  2. LeetCode算法题-Best Time to Buy and Sell Stock II

    这是悦乐书的第173次更新,第175篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Easy级别的第32题(顺位题号是122).假设有一个数组,其中第i个元素是第i天给定股票的价格.设计 ...

  3. Docker卸载镜像

    Linux服务器Docker卸载某个镜像: 首先输入命令docker images查看当前docker下有多少镜像: 1 [root@iZwz9a191mdam4di3dozk3Z ~]# docke ...

  4. nginx配置tomcat负载均衡,nginx.conf配置文件的配置

  5. UVA11093-Just Finish it up（思维）

    Problem UVA11093-Just Finish it up Accept: 1225  Submit: 5637Time Limit: 3000 mSec Problem Descripti ...

  6. 关于connect by rownum与connect by leve

    http://www.itpub.net/forum.php?mod=viewthread&tid=1570306 http://www.itpub.net/forum.php?mod=vie ...

  7. truffle框架的简单使用

    truffle 给大家介绍一下这个框架怎么使用,其实把这个框架就是你们看我之前有一个教程是教你们怎么用remix-ide来连接私有链,编译,配置合约,然后进行调用的,truffle其实就是把这个步骤放 ...

  8. BottomNavigationBar

    重点: bottomNavigationBar: BottomAppBar( shape: CircularNotchedRectangle(),//这个就是设置floatingactionbutto ...

  9. adaboost-笔记(1)

    1 - 加法模型 加法模型,就是通过训练集不断的得到不同的分类器(回归),然后将这些分类器组合成一个新的分类器的过程. 假设有\(N\)个样本,且我们的加法模型如下: \[f(x)=\sum_{m=1 ...

  10. jquery append()与html()注意项

    项目中,涉及到有一部分js代码是从数据库中读取出来动态加载到一个<script>标签中的情况.使用到了jquery的append()和html()两个函数. 应用场景如下: 页面端,有一个 ...