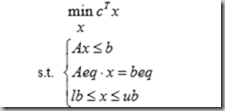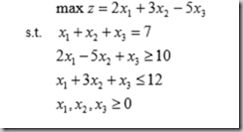【数学建模】day01-线性规划问题
线性规划问题是在一组线性约束条件下,求线性目标函数最大/最小值的问题。这些约束条件有不等式约束、等式约束以及边界约束,这和中学讲的线性规划无异。
此类问题的MATLAB标准形式为:
其中,max问题可以转换为min求解,三个约束条件分别为不等、等式、边界约束。
MATLAB求解函数:
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
param:
c是目标系数;
A、b对应不等条件;
Aeq、beq对用等式条件;
LB、UB为边界;
x0是求解的初始值;
OPTIONS是控制参数,一般不用。
return:
x向量是使得目标函数最小的x取值;
fval是相应的目标函数最优值,若是由max问题转化为min,还要取反。
例题以及matlab求解:
一、求解线性规划问题
求解的matlab程序如下:
f = [-2;-3;5];
A = [-2,5,-1;1,3,1];
b = [-10;12];
Aeq = [1,1,1];
beq = 7;
lb = [0;0;0];
ub = [inf;inf;inf];
[x,y]=linprog(f,A,b,Aeq,beq,zeros(3,1));
x
y = -y二、其他可以转换为线性规划问题,如目标为绝对值函数,指派问题(匈牙利算法),对偶理论与敏感度分析,在此略过,使用时查阅。
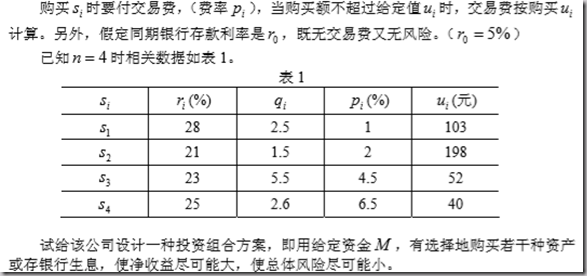
三、应用建模:投资的收益与风险
模型一的求解:
clc,clear
a = 0;
hold on
while a<0.05
c = [-0.05,-0.27,-0.19,-0.185,-0.185]
A = [zeros(4,1),diag([0.025,0.015,0.055,0.026])];
b = a*ones(4,1);
Aeq = [1,1.01,1.02,1.045,1.065];
beq = 1;
LB = zeros(5,1);
[X,Q] = linprog(c,A,b,Aeq,beq,LB);
Q = -Q;
Q
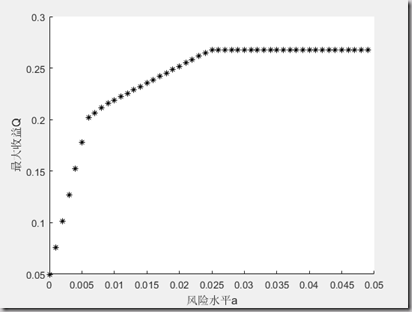
plot(a,Q,'*k');
a = a + 0.001;
end
xlabel('风险水平a');
ylabel('最大收益Q');结果分析:
【数学建模】day01-线性规划问题的更多相关文章
- 【数学建模】线性规划各种问题的Python调包方法
关键词:Python.调包.线性规划.指派问题.运输问题.pulp.混合整数线性规划(MILP) 注:此文章是线性规划的调包实现,具体步骤原理请搜索具体解法. 本文章的各个问题可能会采用多种调用方 ...
- Python数学建模-02.数据导入
数据导入是所有数模编程的第一步,比你想象的更重要. 先要学会一种未必最佳,但是通用.安全.简单.好学的方法. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数据导入 ...
- Python小白的数学建模课-03.线性规划
线性规划是很多数模培训讲的第一个算法,算法很简单,思想很深刻. 要通过线性规划问题,理解如何学习数学建模.如何选择编程算法. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛 ...
- BITED数学建模七日谈之二:怎样阅读数学模型教材
今天进入我们数学建模七日谈的第二天:怎样阅读数学建模教材? 大家再学习数学建模这门课程或准备比赛的时候,往往都是从教材开始的,教材的系统性让我们能够很快,很深入地了解前人在数学模型方面已有的研究成果, ...
- Python数学建模-01.新手必读
Python 完全可以满足数学建模的需要. Python 是数学建模的最佳选择之一,而且在其它工作中也无所不能. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数学 ...
- Python小白的数学建模课-A1.2021年数维杯C题(运动会优化比赛模式探索)探讨
Python小白的数学建模课 A1-2021年数维杯C题(运动会优化比赛模式探索)探讨. 运动会优化比赛模式问题,是公平分配问题 『Python小白的数学建模课 @ Youcans』带你从数模小白成为 ...
- Python小白的数学建模课-04.整数规划
整数规划与线性规划的差别只是变量的整数约束. 问题区别一点点,难度相差千万里. 选择简单通用的编程方案,让求解器去处理吧. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达 ...
- Python小白的数学建模课-A1.国赛赛题类型分析
分析赛题类型,才能有的放矢. 评论区留下邮箱地址,送你国奖论文分析 『Python小白的数学建模课 @ Youcans』 带你从数模小白成为国赛达人. 1. 数模竞赛国赛 A题类型分析 年份 题目 要 ...
- Python小白的数学建模课-05.0-1规划
0-1 规划不仅是数模竞赛中的常见题型,也具有重要的现实意义. 双十一促销中网购平台要求二选一,就是互斥的决策问题,可以用 0-1规划建模. 小白学习 0-1 规划,首先要学会识别 0-1规划,学习将 ...
- Python小白的数学建模课-A3.12 个新冠疫情数模竞赛赛题与点评
新冠疫情深刻和全面地影响着社会和生活,已经成为数学建模竞赛的背景帝. 本文收集了与新冠疫情相关的的数学建模竞赛赛题,供大家参考,欢迎收藏关注. 『Python小白的数学建模课 @ Youcans』带你 ...
随机推荐
- java 基础04 重写
- JavaEE学习之JPA中配置文件persistence.xml
下面是我从网上找到的关于JPA配置文件persistence.xml的相关描述: <?xml version="1.0" encoding="UTF-8" ...
- 史上最全面的Spring Boot Cache使用与整合
一:Spring缓存抽象 Spring从3.1开始定义了org.springframework.cache.Cache和org.springframework.cache.CacheManager接口 ...
- H5 marquee标签
39-marquee标签 内容 属性: direction: 设置滚动方向 left/right/up/down scrollamount: 设置滚动速度, 值越大就越快 loop: 设置滚动次数, ...
- elasticsearch判断索引是否存在
一.判断索引是否存在 指定索引名,判断指定的索引是否存在集群中 /** * 判断指定的索引名是否存在 * @param indexName 索引名 * @return 存在:true; 不存在:fal ...
- openstack-KVM-vCPU
一.KVM基础功能 (1)支持 硬件支持 VT-x VT-d 系统支持 kernel > 3.5 (2)计算机系统的子系统 CPU 处理器 Memory 内存 Storage 存储 Networ ...
- html总结:表格中的文字居中
<style> table { text-align:center; } </style>
- hadoop实例-网站用户行为分析
一.数据集 网站用户购物行为数据集2030万条,包括raw_user.csv(2000万条)和small_user.csv(30万条,适合新手) 字段说明: user_id 用户编号,item_id ...
- CentOS 7 安装配置带用户认证的squid代理服务器
这里只简述搭建一个带用户认证的普通代理 一.安装 安装过程十分简便,只需要安装一下squid,一条命令搞定 yum install squid rpm -qa | grep squid squid-- ...
- 解读event.returnValue和return false
前言 首先我们要清楚returnValue是IE的一个属性,如果设置了该属性,它的值比事件句柄的返回值优先级要高,把它的值设置为false,可以取消发生事件源元素的默认动作:return false就 ...