稀疏矩阵 part 1

▶ 图片参考【http://www.bu.edu/pasi/files/2011/01/NathanBell1-10-1000.pdf】

▶ 各种系数矩阵的数据结构

● MAT，原始矩阵数据

 typedef struct          // 顺序格式
 {
     int     row;        // 行数
     int     col;        // 列数
     int     count;      // 非零元个数（用于转换，不用于计算）
     format  *data;      // 元素的值
 }
 MAT;

●  Compressed Sparse Row（CSR），由非零值向量，各元素列号向量，各行首元在列号向量中的起始位置向量组成

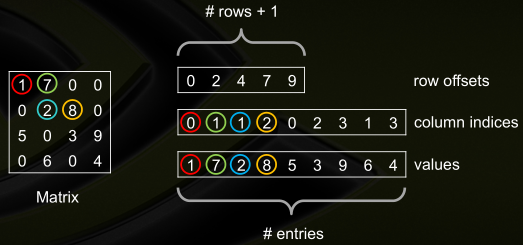
 typedef struct
 {
     int     row;        // 行数
     int     col;        // 列数
     format  *data;      // 非零元的值
     int     *index;     // 非零元的列号
     int     *ptr;       // 每行首元在 index 中的下标，最后一个元素的值等于矩阵非零元个数
 }
 CSR;

● Compressed Sparse Column Format (CSC)，类似 CSR，不过是列优先存储，实现暂时没写，留坑

 typedef struct
 {
     int     row;        // 行数
     int     col;        // 列数
     format  *data;      // 非零元的值
     int     *index;     // 非零元的行号
     int     *ptr;       // 每列首元在 index 中的下标，最后一个元素的值等于矩阵非零元个数
 }
 CSC;

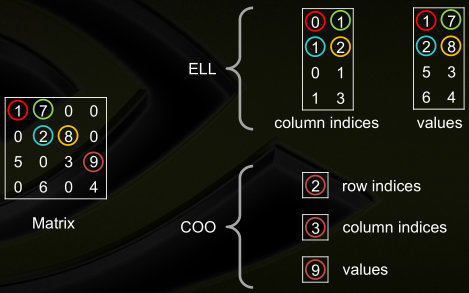
●  ELLPACK（ELL），记录非零元的列号，然后把非零元素压缩到最左边。为了提高内存读取，我的 ELL 相当于将图中的两个矩阵进行了转置

 typedef struct
 {
     int     row;        // 行数，等于 MAT 格式非零元最多行的非零元个数
     int     col;        // 列数，等于 MAT 格式的行数
     int     colOrigin;  // 原列数，等于 MAT 格式的列数
     format  *data;      // 非零元的值
     int     *index;     // 元素在原矩阵中的列号
 }
 ELL;

●  Coordinate（COO），用行列坐标来记录每个非零元的位置

 typedef struct
 {
     int     row;        // 行数
     int     col;        // 列数
     int     count;      // 非零元个数
     int     *rowIndex;  // 行向量
     int     *colIndex;  // 列向量
     format  *data;      // 元素的值
 }
 COO;

● Diagonal（DIA），相当于将矩阵的主对角线捋成一列，其他元素水平移动，然后砍掉所有元素均为零的列（即原矩阵中所有元素均为零的对角线），变换后矩阵行数不变，列数可能增大或减小

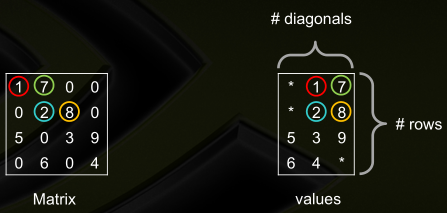
 typedef struct
 {
     int     row;            // 行数
     int     col;            // 列数
     int     colOrigin;      // 原列数
     format  *data;          // 元素的值
     int     *index;         // 原矩阵各对角线是否非零
 }
 DIA;

● Hybrid (HYB) ELL + COO，相当于先尽量 ELL，右边多出的部分砍下来用 COO 单独保存。实现暂时没写，留坑

● Skyline Matrix Storage Format，参考【https://software.intel.com/en-us/mkl-developer-reference-c-sparse-blas-skyline-matrix-storage-format】。实现暂时没写，留坑

■ 例如，下三角中，value 按行优先保存了主对角线及其左下部的元素，每行开头的零略掉但中间的零不省略，ptr 记录每行第一个非零元在 value 中的下标；上三角类似，但是按列优先排列元素。

● Block Sparse Row（BSR），参考【https://software.intel.com/en-us/mkl-developer-reference-c-sparse-blas-bsr-matrix-storage-format】，那个 4 向量的版本没太理解，3 向量的版本参考【http://www.cs.colostate.edu/~mcrob/toolbox/c+/sparse_matrix_compression.html】看懂了。实现暂时没写，留坑

■ 3 向量版本中，value 表示分块小矩阵的值，呈行优先排列，小矩阵元素展开成一维时内部要列优先排列（这里超出了 Mathtype 的最大宽度，所以没有展开），col_index 表示每个小矩阵起始列号，row_ptr 表示每行首个非零小矩阵在 col_index 中的下标