吴恩达机器学习笔记 —— 7 Logistic回归

http://www.cnblogs.com/xing901022/p/9332529.html

本章主要讲解了逻辑回归相关的问题，比如什么是分类？逻辑回归如何定义损失函数？逻辑回归如何求最优解？如何理解决策边界？如何解决多分类的问题？

更多内容参考 机器学习&深度学习

有的时候我们遇到的问题并不是线性的问题，而是分类的问题。比如判断邮件是否是垃圾邮件，信用卡交易是否正常，肿瘤是良性还是恶性的。他们有一个共同点就是Y只有两个值{0,1}，0代表正类，比如肿瘤是良性的；1代表负类，比如肿瘤是恶性的。当然你想用1代表良性也可以，而且输出的值不仅仅局限为0和1两类，有可能还有多类，比如手写体识别是从0到9。

如果使用线性的方法来判断分类问题，就会出现图上的问题。我们需要人工的判断中间的分界点，这个很不容易判断；如果在很远的地方有样本点，那么中心点就会发生漂移，影响准确性。

如果我们想要结果总是在0到1之间，那么就可以使用sigmoid函数，它能保证数据在0-1之间。并且越趋近于无穷大，数据越趋近于1。

回到我们假设的问题上来，如果肿瘤是依赖于大小来判断良性恶性，如果超过0.7*平均值，就判断是恶性的，那么平均来算30%的是恶性的，70%是良性的，他们相加总会是100%。再来看看上面的sigmoid的图像，每个点都表示它属于1的概率是x，属于0的概率是1-x。这样一个分类的问题，就变成了曲线值得问题了。

如果想让y=1，即g(z)的值要大于0.5，那么z的值就需要大于0；相反，y=0，就是z的值小于0。因此整个分类问题，就变成了寻找决策边界的问题了。

那么如何确定逻辑回归的损失函数呢？如果使用均方误差，由于最终的值都是0和1，就会产生震荡，此时是无法进行求导的。

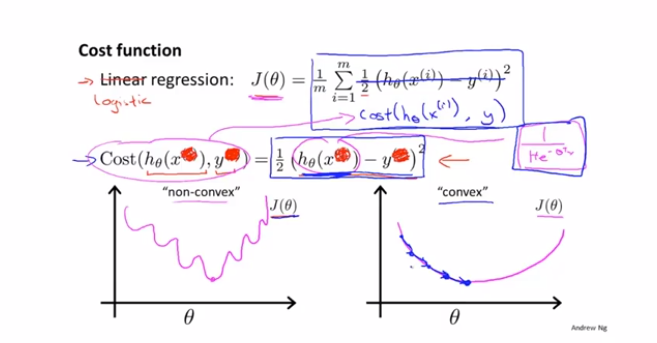
因此需要寻找一个方法，使得代价函数变成凸函数，从而易于求解。

如果把损失函数定义为上面的形式，当真实的值是1时，我们预测的值越靠近1，cost的值越小，误差越小。如果真实值是0，那么预测的值越靠近1，cost的值越大。完美的表达了损失的概念。而且，由于0和1的概念，可以把上面的公式合并成下面统一的写法。直接基于这个统一的写法，做梯度下降求解即可。

在求解最优化的问题时，不仅仅只有一种梯度下降Gradient descenet,还可以使用Conjugate gradient，BFGS，L-BFSGS。

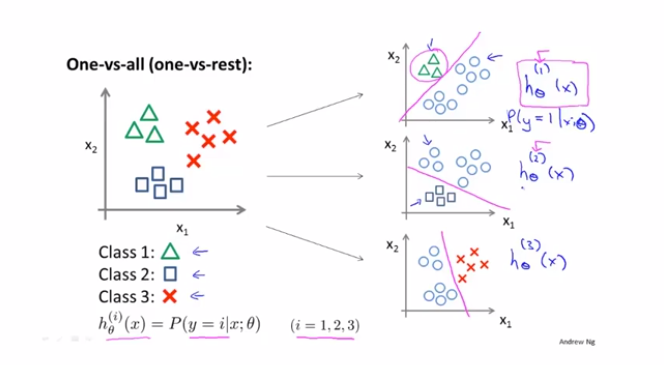
多分类问题，可以理解为采用多个logistic分类器，进行分类。针对每个样本点进行一个预测，给出概率值，选择概率值最高的那个进行分类的标识。