吴恩达机器学习笔记27-样本和直观理解2（Examples and Intuitions II）

二元逻辑运算符（BINARY LOGICAL OPERATORS）当输入特征为布尔值（0 或1）时，我
们可以用一个单一的激活层可以作为二元逻辑运算符，为了表示不同的运算符，我们只需要
选择不同的权重即可。
下图的神经元（三个权重分别为-30，20，20）可以被视为作用同于逻辑与（AND）：

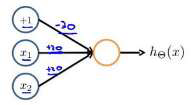
下图的神经元（三个权重分别为-10，20，20）可以被视为作用等同于逻辑或（OR）：

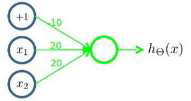
下图的神经元（两个权重分别为 10，-20）可以被视为作用等同于逻辑非（NOT）：

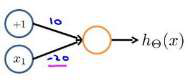
我们可以利用神经元来组合成更为复杂的神经网络以实现更复杂的运算。例如我们要实
现XNOR 功能（输入的两个值必须一样，均为1 或均为0），即：
XNOR = (x1 AND x2) OR((NOT x1)AND(NOT x2))
首先构造一个能表达(NOT x1)AND(NOT x2)部分的神经元：

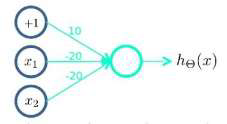
然后将表示 AND 的神经元和表示(NOT x1)AND(NOT x2)的神经元以及表示 OR 的神
经元进行组合：

我们就得到了一个能实现 XNOR 运算符功能的神经网络。
按这种方法我们可以逐渐构造出越来越复杂的函数，也能得到更加厉害的特征值。
这就是神经网络的厉害之处。