[matlab] 22.matlab图论实例 最短路问题与最小生成树 (转载)

最短路问题之 Floyd

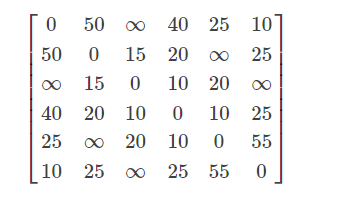
某公司在六个城市 c1c1,c2c2,….,c6c6 中有分公司，从 cici 到 cjcj 的直接航程票价记在下述矩阵的 (ii,jj) 位置上。 （∞∞表示无直接航路），请帮助该公司设计一张城市 c1c1 到其它城市间的票价便宜的路线图。

变量解释：

• n 是公司个数
• a 存储航路票价，最后结束循环存储的是最便宜票价
• path 存储每对顶点之间最短路径上所经过的定点的序号，也就是”中转站”序号

clear;clc;
n = 6;
a = [0 50 inf 40 25 10;
        0 0 15 20 inf 25;
        0 0 0 10 20 inf;
        0 0 0 0 10 25;
        0 0 0 0 0 55;
        0 0 0 0 0 0];  % 由于 a 是无向图，航路票价沿着正对角线对称，可以只写出右上角
a = a + a';    % 由于票价沿正对角线对称，即完整的 a 为 a + a 的转置
path = zeros(6);   % 定义 path 为 6 x 6 的矩阵
for k = 1:n
      for i = 1:n
        for j = 1:n
          if a(i,j) > a(i,k) + a(k,j)
          % 如果从 i 城市到 j 城市的票价大于从 i 城市到 k，再从 k 到 j 城，那么 i 到 j 城肯定不是最短路径
             a(i,j)  =  a(i,k) + a(k,j);    % 更新 i 到 j 的最少票价
             path(i,j) = k;     % 同时记录下 i 到 j 的"中转站"
             % 注意下一次更新会覆盖上一次 path(i,j) 存储的，所以其实 path(i,j)中存储的 只是最后一个 "中转站"
          end
        end
      end
  end
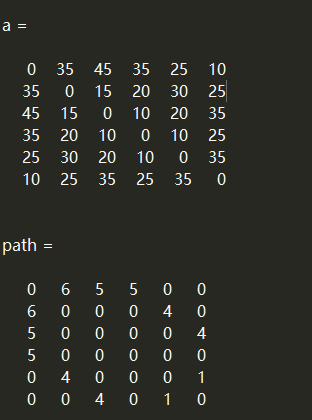
a,path

Floyd 算法

最短路问题之 dijkstra 算法

变量解释：

• n 是公司个数
• m 存储票价
• pb 存放标号信息，当 pb(ii) = 1，当前第 ii 节点已标号，否则为 0 未标号
• d 表示最短通路的值
• path 存储每对顶点之间最短路径上所经过的定点的序号
• tb 表示当前未标记的点的矩阵
• fb 表示当前已标记的点的矩阵
• min 求最小值之前的预设值
• lastpoint 暂存当前选定的一个已标记点
• newpoint 暂存当前选定的一个未标记点
• plus 即已知点到未知点距离

clear;clc;
n = 6;
m = [0 50 inf 40 25 10;
     0 0 15 20 inf 25;
     0 0 0 10 20 inf;
     0 0 0 0 10 25;
     0 0 0 0 0 55;
     0 0 0 0 0 0];
 m = m + m';
 pb(1:length(m))= 0; % 将所有未标记点置 0
 pb(1) = 1;    % 选择第 1 个点标记
 d(1:length(m))=0;  % 将全部最短距离置 0
 path(1:length(m))=0;   % 将全部"中转站"置 0
 while sum(pb) < 6  % 当状态不全为 1（即未标记全部点时）
     tb = find(pb==0);   % 找到未标记的点的矩阵
     fb = find(pb==1);   % 找到已标记的点的矩阵
     min = 1000000;
     lastpoint =1;
     newpoint =1;
     % 从每一个已标记点，到每一个未标记点
     for i=1:length(fb)
         for j=1:length(tb)
             plus = d(fb(i)) + m(fb(i),tb(j));  % 计算点之间的距离
             if min > plus
                min = plus;  % 更新最小值
                lastpoint = fb(i);   % 记录当前最小值下已标记点
                newpoint = tb(j);    % 记录当前最小值下未标记点
             end
         end
     end
     d(newpoint) = min;   % 更新最终的最小值
     pb(newpoint) = 1;    % 更新当前未标记点状态（未标记——》标记）
     path(newpoint) = lastpoint;  % 更新当前点上一个点
 end
 d,path

dijkstra 算法

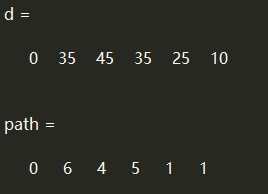
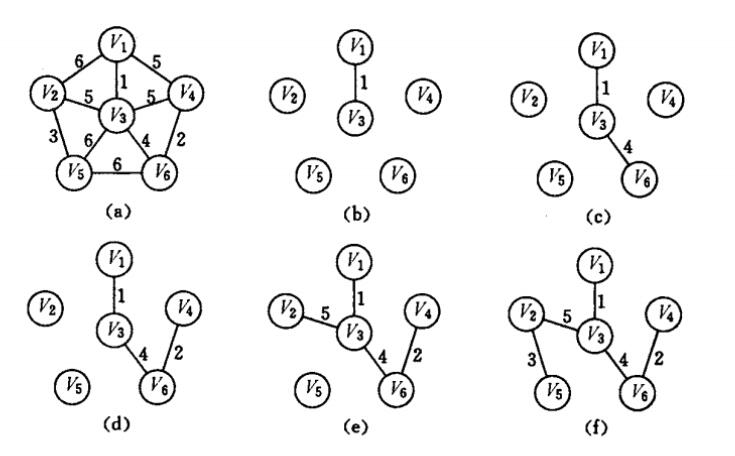
最小生成树问题之prim

变量解释：

• n 顶点个数
• a 存储图
• result 第一、二、三行分别表示生成树边的起点、终点、权集合
• p 存放图的最小生成树中的顶点
• tb 存放当前未选择的顶点
• temp 存放当前最小生成树连通的所有边
• d 存放最小的边值
• jb 存放最小的边值中已经选作最小生成树的点的矩阵（也许不止一个）
• kb 存放最小的边值中未选作最小生成树的点的矩阵（也许不止一个）
• j 确定已经选作最小生成树的点的矩阵中的第一个点
• k 确定未被选作最小生成树的点的矩阵中的第一个点

clear;
clc;
n = 7;
a = [0 50 60 inf inf inf inf;
     0 0 inf 65 40 inf inf;
     0 0 0 52 inf inf 45;
     0 0 0 0 50 30 42;
     0 0 0 0 0 70 inf;
     0 0 0 0 0 0 inf;
     0 0 0 0 0 0 0];% 由于 a 是无向图，航路票价沿着正对角线对称，可以只写出右上角
a = a + a';    % 由于票价沿正对角线对称，即完整的 a 为 a + a 的转置
result =[];   % 定义出 result
p =1;   % 当前只有第 1 个点为最小生成树的节点
tb =2:n;   % 当前未作为最小生成树的节点
while length(result) ~= n - 1   % 当生成树的边为 节点数-1 时，即最小生成树生成（n个点 n-1 条边）
    temp = a(p,tb);  % 存放当前最小生成树连通的所有边，用来求最短边
    temp = temp(:);   % 将 temp 转化成 1 列，让求出的最短距离只有一个值
    d = min(temp);  % 求出最短距离
    [jb,kb] = find(a(p,tb)==d);  % 根据最短距离，找出哪些点符合最短距离的情况
    j = p(jb(1));    % 从当前最小生成树中的点中
    k = tb(kb(1));   % 和当前未进入最小生成树的点中挑出第一个点
    result = [result,[j;k;d]];   % 表示生成树边的起点、终点、权集合
    p = [p,k];   % 刚刚选的点进入最小生成树
    tb(find(tb==k)) =[];    % 将进入最小生成树的点剔除掉
end
result

prim 算法

最小生成树问题之kruskal (待补充)