P3472 [POI2008]MAF-Mafia

P3472 [POI2008]MAF-Mafia

解法

不难发现，这个题目建图后出现的是一个基环树森林+一堆环，因为每个点仅有一条出边。

大概长这样：

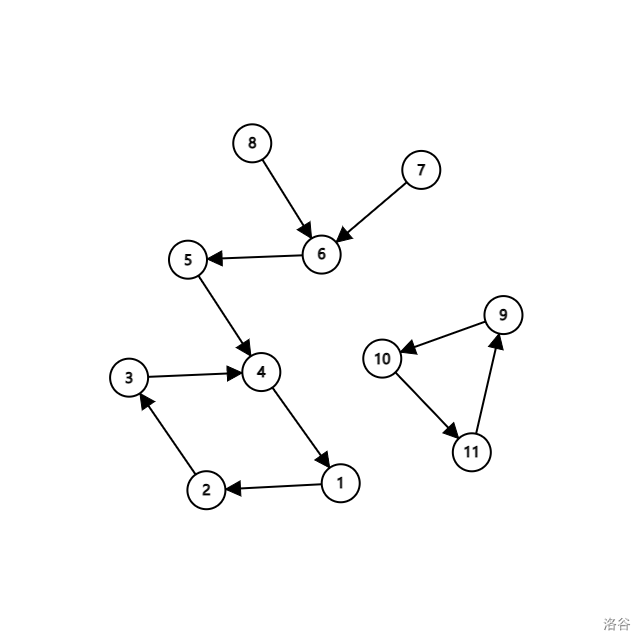
对于最大，最小值，我们分开考虑。

最大值

可以看到，当我们缩点后，对于一个没有入度的点，其对答案的贡献为1。

因为当一个点入度为0时，其要么原本是个环，要么原本也是一个点：

当其是一个环时，可以通过一些击杀顺序从而使环仅剩一个点。

当其是一个点时，没有点可以杀掉他。

而其他点都可以通过一些奇妙的顺序被杀掉。

最小值

我们观察，如果是一个单独的环，其对答案的贡献应该是\(siz/2\)

我们再在一颗基环树上观察：

可以得到，入读为\(0\)的点是不会被杀的，那么我们将其入队，并统计答案。

然后入读为\(0\)的点所指向的点一定会被杀，当我们将队头取出时，将其所指向的点杀掉，再将其指向的点所指向的点的入读减\(1\)，当其入度为\(0\)时，便将其入队，并统计答案。

这里就相当于做了一次变形的拓扑排序。

然后我们再去找环：

当这个环上至少有一个点被杀时，那么这个环就变成链，再拓扑排序的时候已经计算过了不管。

如果没有点被杀，则和单独一个环的情况一样。

CODE

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e6+33;
inline ll read_int(){
	ll a=0;bool f=0;char g=getchar();
	while(g<'0'||'9'<g) {if(g=='-') f=1;g=getchar();}
	while('0'<=g&&g<='9') a=a*10+g-'0',g=getchar();
	return f ? -a : a;
}

inline void write(ll a,bool b=1){
	if(a<0) a=-a,putchar('-');
	int lin[30],top=0;
	while(a) lin[++top]=a%10,a/=10;
	if(top==0) lin[++top]=0;
	while(top) putchar(lin[top--]+'0');
	if(b) putchar('\n');
}
int n;
int t[maxn],rd[maxn];

int tme,low[maxn],dfn[maxn],zan[maxn],top;
int bel[maxn],siz[maxn],tot;
int vis[maxn];

inline void tarjian(int s){
	low[s]=dfn[s]=++tme;
	zan[++top]=s;
	if(!vis[t[s]]){
		if(dfn[t[s]]) low[s]=min(low[s],dfn[t[s]]);
		else tarjian(t[s]),low[s]=min(low[s],low[t[s]]);
	}
	vis[s]=1;
	if(low[s]==dfn[s]){
		tot++;
		while(zan[top]!=s){
			siz[tot]++;
			bel[zan[top]]=tot;
			top--;
		}
		siz[tot]++;
		bel[zan[top]]=tot;
		top--;
	}
}

int maxx=0,rd_[maxn];

inline void suodian(){
	for(int i=1;i<=n;i++){
		if(rd[i]==0) maxx++;
		if(bel[i]==bel[t[i]]){
			if(i==t[i]) rd_[bel[i]]=1;
			continue;
		}
		rd_[bel[t[i]]]++;
	}
	for(int i=1;i<=tot;i++){
		if(rd_[i]) continue;
		if(siz[i]==1) continue;
		maxx+=1;
	}
	maxx=n-maxx;
}

int die[maxn],dee[maxn];
inline void read(){
	n=read_int();
	for(int i=1;i<=n;i++) t[i]=read_int(),rd[t[i]]++;
	for(int i=1;i<=n;i++) if(vis[i]==0) tarjian(i);
	suodian();
	queue<int> p;
	ll minn=0;
	for(int i=1;i<=n;i++){
		if(rd[i]) continue;
		minn++;
		p.push(i);
	}
	while(!p.empty()){
		int s=p.front();
		p.pop();
		if(die[t[s]]) continue;
		die[t[s]]=1;
		if((--rd[t[t[s]]])==0) p.push(t[t[s]]),minn++;
	}
	for(int i=1;i<=n;i++) dee[bel[i]]|=die[i];
	for(int i=1;i<=tot;i++) if(dee[i]==0&&siz[i]>1) minn+=siz[i]/2;
	cout<<n-minn<<" "<<maxx;
}

int main (){
	// freopen("maf.in","r",stdin);
	// freopen("maf.out","w",stdout);
	read();
	// while(1) getchar();
}

后记

模拟赛没写出来，木有判断自环。。。。